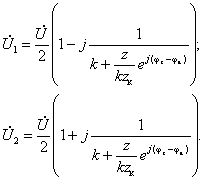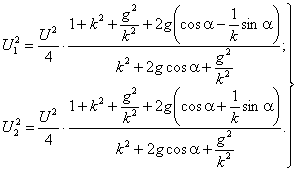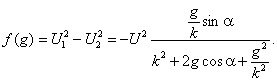Введем в (3-226) обозначения:  и ; после этого получим:

          (3-227)

Далее обозначим , полагая g переменным, но j_z при этом будем считать постоянным: например, если в фазу b включается активное сопротивление, то j_z = 0 = const, если конденсатор, то j_z =  = const. При включении в фазу b реактивной катушки также будем считать, что для нее  = tg j_z = const.

При g = 0 внешнее сопротивление Z = 0, чему соответствует непосредственное подключение фазы b к сети. Согласно (3-227) в этом случае модули  и  равны между собой ( при k = 1) и, следовательно, моменты от прямого и обратного полей одинаковы и М_нач = 0.

При g = ¥, Z = ¥ фаза b разомкнута и машина превращается в однофазную, не создающую никакого момента в начале пуска. Для этого случая U₁ =U₂ = U/2.

Найдем теперь, при каком значении g момент М_нач будет максимальным. Для этого надо определить максимум функции , так как М_нач пропорционален . Преобразим уравнения (3-227), подставляя в них  и  и учитывая, что  и  ( и  – векторы, сопряженные с  и ):

          (3-228)

Отсюда получим

          (3-229)

Согласно условию  величина  будет максимальной при g = k², т. е. при z = k²z_к.

Таким образом, мы нашли, что для любой машины при ее пуске в ход с использованием вспомогательной фазы максимальный момент M_нач.м получается в том случае, если абсолютное значение активного, индуктивного или емкостного сопротивления, включаемого во вспомогательную фазу, для данного k равно k²z_к.

Обозначим через M_g начальный вращающий момент, развиваемый машиной, если к ней подводится симметричная двухфазная система напряжений  или если тогда при g = k² будем иметь:

          (3-230)

M_нач.м зависит от . Очевидно, при  момент М_нач = 0. В обычных случаях близкие к этому условия получились бы при включении во вспомогательную фазу реактивной катушки. Однако для очень малых двигателей при cosj_к > 0,6÷0,7 она может найти себе применение, если требуется небольшой M_нач.

Вверх

Глава 4