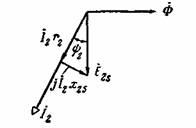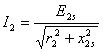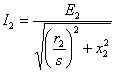Намагничивающая сила ротора при его вращении совместно с н.с. статора создает основное толе. Очевидно, что точно такое же поле будет создаваться в машине и при неподвижном роторе, если токи в его обмотке по величине и фазе (относительно э.д.с.) остаются теми же, что и при вращении.

На рис. 3-32 представлена векторная диаграмма роторной цепи при s>0, соответствующая уравнению напряжений (3-85). 

Рис. 3-32. Векторная диаграмма роторной цепи при s > 0.

Из этого уравнения находим:

.          (3-86)

Если числитель и знаменатель правой части равенства разделить на s, то получим тот же ток

,          (3-87)

где Е₂ и х₂ — э.д.с. и индуктивное сопротивление рассеяния роторной цепи при неподвижном роторе.

Таким образом, вместо вращающегося ротора можно рассматривать неподвижный ротор, но при этом необходимо считать активное сопротивление его цепи равным . В этом случае ток роторной цепи I₂ остается тем же самым, что и при скольжении s, так же как и сдвиг его по фазе ψ₂ относительно э.д.с. (рис. 3-32 и 3-33).

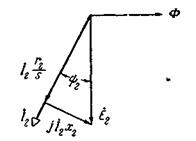
Рис. 3-33. Векторная диаграмма роторной цепи при неподвижном роторе.

Теперь мы можем перейти от вращающегося ротора к неподвижному (эквивалентному), взяв здесь только фазы статора и ротора, оси которых совпадают, и рассматривать работу машины как работу условного трансформатора, первичная (статорная) и вторичная (роторная) обмотки которого пронизываются одновременно одним и тем же главным потоком Ф (рис. 3-34). При этом необходимо, чтобы н.с. обмоток по амплитуде были равны F₁ и F₂ и чтобы эти н.с. по фазе (во времени) были сдвинуты на такой же угол, на который они были сдвинуты в пространстве при работе машины двигателем.

Вверх

Глава 4