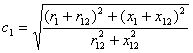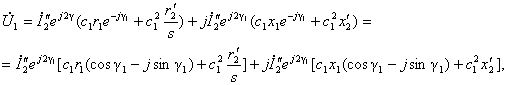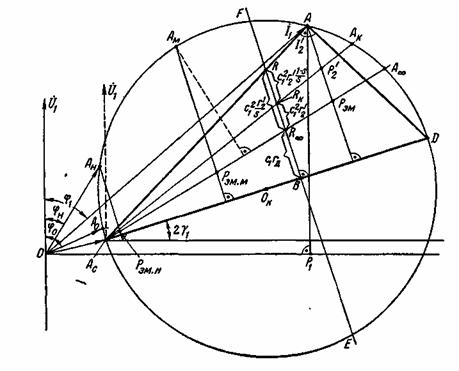
Круговая диаграмма асинхронной машины представляет собой геометрическое место концов вектора тока , изменяющегося при изменении скольжения s в пределах от + ∞ до -∞, если при этом напряжение на зажимах статора машины и все ее параметры сохраняют постоянные значения. Ее называют также диаграммой тока. Она дает наглядное представление о важных зависимостях между величинами, характеризующими работу асинхронной машины.

Обратимся к схеме замещения, представленной на рис. 3-49. Введем обозначение:

.          (3-169)

Тогда в соответствии со схемой замещения и уравнениями (3-120) и (3-121) можем написать:

.          (3-170)

Комплексный коэффициент C₁ согласно (3-126) равен:

,          (3-171)

где

          (3-172)

и

.          (3-173)

Подставив в (3-170) значение C₁ по (3-171), будем иметь:

что после преобразований дает:

,          (3-174)

где

;          (3-175)

.          (3-176)

Разделив (3-174) на , получим:

.          (3-177)

Три вектора полученного уравнения токов образуют при токе , соответствующем некоторому скольжению s, прямоугольный треугольник A_cAD, представленный на рис. 3-53, где вектор  направлен по вертикали. В этом треугольнике катеты  и , и гипотенуза  (в соответствии с обычными соотношениями между параметрами асинхронной машины принято, что угол γ₁ имеет отрицательное значение).

Рис. 3-53. Круговая диаграмма асинхронной машины.

Вверх

Глава 4