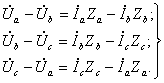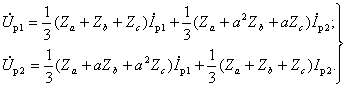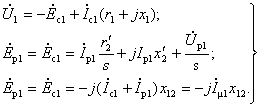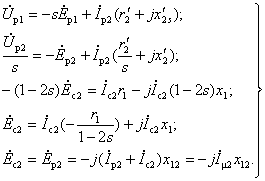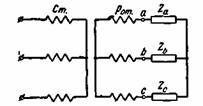
Исследование работы трехфазного асинхронного двигателя при несимметрии фаз ротора будем проводить применительно к двигателю с контактными кольцами, имеющему в роторе трехфазную обмотку.

Рис. 3-76. Схема двигателя с неравными сопротивлениями фаз ротора.

Обратимся к рис. 3-76. Для роторных целей можем написать следующие уравнения напряжений:

          (1-192)

Заменим напряжения и токи их симметричными составляющими, учтя при этом что составляющие нулевой последовательности отсутствуют. Обозначим составляющие прямой и обратной последовательностей в, фазе ротора а соответственно через   и   При этом будем считать, что все величины ротора приведены к обмотке статора.

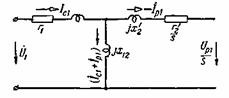
Рис. 3-77. Схема замещения. соответствующая токам прямой последовательности ротора.

Решая полученную систему уравнений в отношении  и , получим:

         (3-193)

Теперь можем написать уравнения напряжений статора и ротора прямой последовательности:

          (3-194)

Уравнениям (3-194) соответствует схема замещения для напряжений и токов прямой последовательности, представленная на рис. 3-77.

Уравнения напряжений ротора и статора обратной последовательности имеют следующий вид:

          (3-195)

Мы считаем, что напряжение  приложено к обмотке ротора, вращающегося со скольжением s относительно основного поля. Рассматривая работу машины, получающей питание со стороны ротора (к обмотке ротора приложено напряжение U_р2 переменной частоты sf₁), видим, что при s > 0,5 машина работает двигателем, так как ротор при этом вращается медленнее, чем обратное поле, а при s < 0,5 машина работает генератором, так как в этом случае ротор вращается быстрее, чем обратное поле.

В последних трех уравнениях (3-195) E_c2 — э. д. с статора, которая наводится в его обмотке обратным полем, т. е. полем токов I_р2 и I_с2, при s = l. При s  1 э. д. с. E_с2(1 - 2s) имеет частоту (1 - 2s)f₁ так же как и вызываемый ею ток I_с2.

Вверх

Глава 4