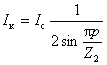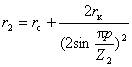б) Активные сопротивления обмоток.

 Сопротивление постоянному току фазы обмотки статора или фазного ротора рассчитывается, Ом,

          (3-157)

где w — число последовательно соединенных витков;

а — число параллельных ветвей;

l_ср — средняя длина витка, м;

s_n — сечение проводника, мм².

Активное сопротивление r₁ обмотки статора будет несколько больше рассчитанного по (3-157). Оно должно учитывать не только потери от прохождения тока по обмотке, но и потери, вызванные полями рассеяния статора. Однако различие между активным сопротивлением и сопротивлением постоянному току обмотки статора обычно невелико и можно принять r₁ = r, а потери, вызванные полями рассеяния, учесть отдельно при определении к.п.д. машины.

Значение сопротивления в относительных единицах измерения (о.е.)  соответственно при Р_н = 0,4-7-600 кВт.

Активное сопротивление r₂ обмотки фазного ротора при нормальных режимах работы двигателя (при s < 5  10%) может быть принято равным сопротивлению постоянному току. При больших скольжениях для двигателей, имеющих на роторе двухслойную стержневую обмотку (при глубине паза примерно свыше 2 см), r₂ заметно возрастает.

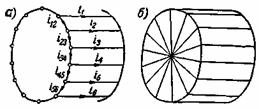
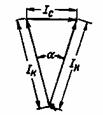
Покажем, как рассчитывается сопротивление r₂ короткозамкнутой обмотки, выполненной в виде беличьей клетки. Такую клетку можно рассматривать как многофазную обмотку, имеющую число фаз m₂, равное числу пазов ротора Z₂, причем здесь в каждую фазу входит один стержень. На рис. 3-50,а схематически изображена обмотка в виде клетки.  

Рис. 3-50. Беличья клетка и эквивалентная ей обмотка.

Здесь показаны токи в стержнях и частях короткозамыкающего кольца, лежащих между серединами соседних стержней. Эти части следует считать за сопротивления, соединенные многоугольникам. Поэтому токи в стержнях i₁, i₂, i₃,… должны рассматриваться как линейные, а токи в частях кольца , i₁₂, i₂₃, i₃₄,… — как фазные. В соответствии с этим на рис. 3-51 построена векторная диаграмма токов в соседних частях кольца I_к и в стержне I_с.

Рис. 3-51. Векторная диаграмма токов в стержне I_с и соседних частях кольца.

Сдвиг по фазе токов в соседних стержнях и частях кольца равен:

.          (3-158)

Из векторной диаграммы находим соотношение между I_к и I_с:

.          (3-159)

Для расчета заменим сопротивления частей кольца, соединенные многоугольником, сопротивлениями, соединенными звездой, после чего получим эквивалентную обмотку, показанную на рис. 3-50,б. Сопротивление фазы r₂ такой обмотки принимается за сопротивление фазы беличьей клетки Оно определяется из равенства

,          (3-160)

где r_с — сопротивление стержня; r_к — сопротивление части кольца между соседними стержнями. Сопротивления r_с и r_к определяются по геометрическим размерам стержня и кольца и удельному сопротивлению материала, примененного для клетки (например, для литого алюминия .

Из (3-160) и (3-159) имеем:

.          (3-161)

Приведение сопротивления r₂ к обмотке статора делается по формуле

,          (3-162)

так как m₂ = Z₂, w₂ = 1/2, k₀₂ = 1. Здесь также при малых скольжениях (s < 5  7%)r₂, может быть принято равным сопротивлению постоянному току При больших скольжениях оно заметно возрастает, особенно при глубоких пазах на роторе (§ 3-19,в).

В обычных случаях значение r₂ близко к значению r₁.

Вверх

Глава 4