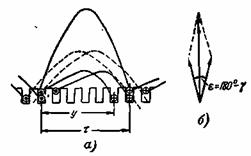
При двухслойных обмотках, которые выполняются обычно с укороченным шагом, необходимо при определении н.с. учесть укорочение шага. На рис. 3-24,а показана часть одной фазы двухслойной обмотки с укороченным шагом. Рассматривая токи верхнего и нижнего слоев, можно установить, что верхние и нижние слои как бы образуются из катушек шириной t (см. также рис. 3-15), причем эти катушки образуют группы, оси которых сдвинуты на угол  эл. град.

Рис. 3-24. Намагничивающая сила одной фазы двухслойной обмотки.

Следовательно, н.с. одной фазы двухслойной обмотки на один полюс равна:

         (3-37)

где  — амплитуда н.с. "катушечной группы" верхнего или нижнего слоя;

w_к  — удвоенное число витков катушки двухслойной обмотки;

k_у1 — коэффициент укорочения, который рассчитывается по (3-10), как и для э.д.с., что следует из рис. 3-24,б.

Заменяя  через  где w — число последовательно соединенных витков фазы обмотки, и учитывая, что аI_к = I — ток этой фазы, получим:

          (3-38)

где k₀₁=k_р1k_у1  обмоточный коэффициент для первой гармоники н.с.

Для амплитуды n-й гармоники н.с. мы можем написать:

          (3-39)

где k_0ν — обмоточный коэффициент для ν-й гармоники н.с., который определяется, так же как для ν-й гармоники э.д.с., по (3-26) — (3-28).

Из табл. 3-1 можно видеть, что укорочение шага позволяет значительно снизить амплитуды высших гармоник в кривой н.с. При y = 0,83t наиболее заметно уменьшаются амплитуды пятой и седьмой гармоник, следующие по величине после третьей гармоники, а так как последняя пропадает в н.с. трехфазной обмотки (см. § 3-4,б), то обычно и выбирают указанное значение шага у. Пульсирующую по оси фазы н.с., синусоидально распределенную и имеющую при максимальном токе  амплитуду F_мq1, можно заменить двумя синусоидально распределенными н.с., но вращающимися в разные стороны с одинаковыми частотами и имеющими неизменные амплитуды F_мq1 что доказывается следующим образом.

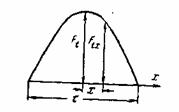
Обратимся к рис. 3-25, где показана кривая пульсирующей н.с. с амплитудой F_t1 = F_мq1sinωt, соответствующей моменту t, когда ток в фазе равен Isinωt. 

Рис. 3-25. Кривая пульсирующей н.с.

Значение н.с., соответствующей точке окружности статора, сдвинутой на x относительно оси фазы, будет:

          (3-40)

Равенство (3-40) согласно известному уравнению

может быть записано в следующем виде:

          (3-41)

Первое слагаемое правой части обозначим через F':

          (3-42)

Полученное уравнение называется уравнением бегущей волны. Оно показывает, что н.с.  является функцией времени t и места х. Если принять, что выражение в скобках равняется постоянной величине с (изменение t компенсируется изменением х), то мы найдем, с какой частотой будет перемещаться н.с. Действительно, дифференцируя уравнение  по t, получим: а отсюда

          (3-43)

С такой частотой будет перемещаться любое значение н.с., а следовательно, и ее амплитуда  Так как при вращательном движении перемещение на 2t соответствует  части оборота, то частота вращения волны н.с. (ее первой гармоники),об/с,

и ─ в об/мин,

.          (3-44)

Вверх

Глава 4