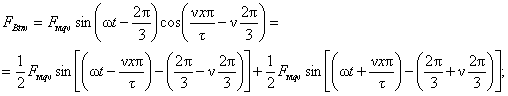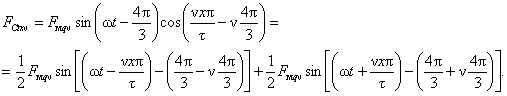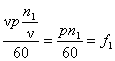Уравнения (3-58) и (3-59) получены для первых гармоник н.с. Они и используются в общей теории машин при определении их рабочих свойств, высшими гармониками при этом пренебрегают, так как амплитуды их незначительны.

Однако для более подробного изучения свойств машин необходимо выяснить, от чего зависят амплитуды высших гармоник н.с. обмоток и с какой частотой они вращаются относительно статора или ротора.

Обратимся к трехфазной обмотке, синусоидальные токи которой образуют симметричную трехфазную систему, и будем при определении ν-й гармоники ее н.с. в точке x (рис. 3-27) учитывать, что по фазе (во времени) ν-е гармоники н.с. фаз В и С сдвинуты относительно v-й гармоники н.с. фазы А на углы  и , так же как соответствующие токи в фазах обмотки, и что оси фаз B и С сдвинуты относительно оси фазы А на углы  и  эл. рад. (для ν-й гармоники t соответствует νπ эл. рад). Следовательно ν-ю гармонику н.с. трехфазной обмотки в точке х получим как сумму ν-х гармоник н.с. фаз в той же точке, выражения для которых в соответствии с (3-48) и (3-49) имеют следующий вид:

;

Приведенные равенства позволяют сделать следующие выводы.

1. В кривой результирующей н.с. трехфазной обмотки все гармоники с номером, кратным трем, пропадают. В этом мы можем убедиться, обращаясь к первой форме выражения для ν-х гармоник н.с. фаз (произведение синуса на косинус). Для всех трех фаз мы будем иметь косинусы одного и того же угла ; сумма же синусоид, сдвинутых на углы  и  и имеющих одинаковые амплитуды, равна нулю.

2. Все гармоники с номером ν = 6а—1, где а — любое целое число (1, 2, 3, ...), при сложении дают ν-ю гармонику, вращающуюся с частотой , т. е. против вращения первой гармоники. В этом мы можем убедиться, обращаясь ко второй форме выражения для ν-х гармоник н.с. фаз (сумма синусов). Подставляя здесь ν = 5, 11, 17 и т. д., мы получим.

,

откуда видим, что ν-я гармоника вращается с частотой  [ср. с (3-58)].

3. Все гармоники результирующей н.с. с номером ν = 6a + 1  вращаются c частотой  в ту же сторону, что и первая гармоника. В этом случае имеем:

.

4. Поля, созданные высшими гармониками н.с. обмотки, будут наводить в этой обмотке э.д.с той же частоты, что и частота э.д.с., наведенной первой гармоникой поля. Действительно, ν-я гармоника вращается с частотой , но она имеет число пар полюсов νр, следовательно, частота наведенной ею э.д.с. равна . Очевидно, получится тот же результат, если учесть, что потокосцепление фазы обмотки, созданное токами частоты f₁ будет во времени изменяться также с частотой f₁.

При несимметричной системе токов в фазах трехфазной симметричной обмотки определяются н.с., созданные каждой из симметричных составляющих данной системы токов. Токи прямой и обратной последовательностей создадут круговые н.с , вращающиеся в разные стороны. Результирующей этих н.c. будет эллиптическая вращающаяся н.с., т. е. пространственный вектор результирующей н.с. будет описывать эллипс. Для определения н.с., созданной токами нулевой последовательности, обратимся к предыдущим выражениям для н.с. отдельных фаз. Так как токи нулевой последовательности равны между собой и совпадают по фазе, то эти выражения будут иметь следующий вид:

;

;

.

Складывая приведенные значения н.с. отдельных фаз, получим результирующую н.с. F_txv в точке х. Для всех значений ν, не кратных трем, F_txv = 0; для значений ν, кратных трем,

.

Следовательно, токи нулевой последовательности будут создавать пульсирующую н.с. с пространственным периодом , где ν = 3, 9, 15 и т. д. Для исследования ее действия она может быть заменена двумя круговыми н.с. с тем же пространственным периодом, вращающимися в разные стороны и имеющими половинную амплитуду.

Вверх

Глава 4