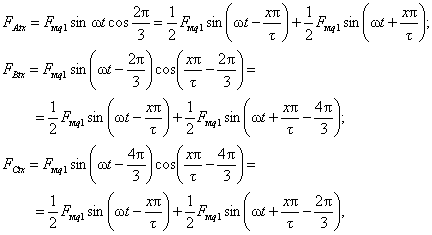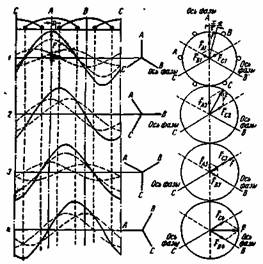
б) Многофазная обмотка.

 Вначале найдем н.с. трехфазной обмотки. Она может быть найдена графически, путем сложения н.с. отдельных фаз с учетом пространственного сдвига осей фаз и сдвига во времени их токов.

На рис. 3-27 слева показано сложение первых гармоник н.с. фаз трехфазной обмотки для отдельных моментов времени.

Рис. 3-27. Намагничивающая сила трехфазной обмотки.

В результате сложения получается синусоидально распределенная н.с. с неизменной амплитудой, в 1,5 раза большей максимальной амплитуды н.с. фазы:

.          (3-52)

К тому же результату можно прийти, рассматривая синусоидально распределенную н.с. каждой фазы как пространственный вектор, выходящий из центра внутренней окружности статора и совпадающий с осью данной фазы. Пространственные векторы пульсирующих н.с. фаз обмотки , ,  (n=l, 2, 3, 4) показаны на рис. 3-27 справа. Их мгновенные значения и направления соответствуют мгновенным значениям и направлениям токов в фазах обмотки. Складывая векторы н.с. , ,  для отдельных моментов времени, получим результирующий пространственный вектор , неизменный по величине, но вращающийся в определенном направлении.

Мы видим, что вектор результирующей н.с. вращается в направлении от A к В и к С. При этом амплитуда н.с. совпадает с осью той фазы, ток которой в данный момент времени имеет максимальное значение. Положительные максимальные значения токов в фазах устанавливаются сначала в фазе А, затем в фазе В и, наконец, в фазе С. Этим определяются порядок чередования фаз и направление вращения амплитуды результирующей н.с.

Изменив порядок чередования фаз путем перемены мест двух проводов, подводящих ток к обмотке статора асинхронного двигателя, мы изменим направление вращения н.с. и создаваемого ею поля, а следовательно, направление, вращения ротора двигателя.

Из рис. 3-27 видно, что за четверть периода изменения тока результирующая н.с. пройдет 0,5t, а за период — 2t. Следовательно, ее линейная скорость перемещения v₁ = 2tf₁, а частота вращения, об/мин,

.          (3-53)

То же самое в общем виде можно доказать, обращаясь к аналитическим выражениям н.с. отдельных фаз. Для этого найдем н.с. фаз A, В, С в точке, сдвинутой на х относительно оси фазы А (рис. 3-27). Фаза А создает в этой точке н.с.

,          (3-54)

Так как токи в фазах В и С относительно тока в фазе А сдвинуты по фазе (во времени) на углы  и  рад, а оси фаз В к С относительно оси фазы А сдвинуты на и  эл. рад., то н.с. фаз В и С в тот же момент времени в рассматриваемой точке равны:

;          (3-55)

.          (3-56)

Если сложить найденные значения н.с., заменив при этом каждую пульсирующую н.с. двумя вращающимися в разные стороны (3-41):

          (3-57)

то получим результирующую н.с.

,          (3-58)

где сумма вторых слагаемых (3-57) равна нулю, так как они представляют собой синусоиды с равными амплитудами, сдвинутые на  и  рад.

Уравнение (3-58) — уравнение бегущей волны, перемещающейся с частотой v₁ = 2tf₁ или вращающейся с частотой  [ср. с (3-42) и (3-44)].

Таким образом, мы доказали, что результирующая н.с. трехфазной обмотки при наличии в ней трехфазного тока является н.с. с неизменной амплитудой , вращающейся с частотой n₁.

Если стальные участки магнитной цепи ненасыщены, то кривая н.с. в другом масштабе дает нам кривую поля машины, которая, так же как и кривая н.с., вращается при неизменной амплитуде с частотой п₁. Такое поле называется круговым вращающимся полем.

В общем случае симметричная m-фазная обмотка при наличии в ней симметричного m-фазного тока создает вращающуюся н.с. с постоянной амплитудой

,          (3-59)

которую аналогично предыдущему можно найти графически или аналитически путем сложения н.с. отдельных фаз.

Вверх

Глава 4