Обозначив второе слагаемое равенства (3-41) через F", мы также получим уравнение бегущей волны:

.          (3-45)

Однако частота ее перемещения и , найденная аналогичным образом, будет отрицательной:

,          (3-46).

так же как и частота вращения, об/мин,

.          (3-47)

Это значит, что н.с.  перемещается в обратную сторону (положительному приращению dt соответствует отрицательное приращение dx).

Таким образом, мы получили две вращающиеся н.с., которые можно изобразить вращающимися пространственными векторами  и  (рис. 3-26).

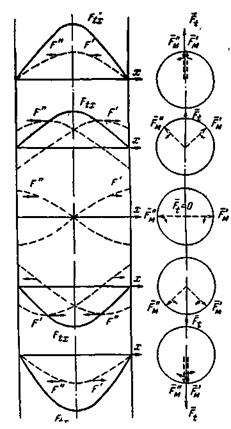
Рис. 3-26. Замена пульсирующей н.с. двумя круговыми вращающимися н.с.

Пространственным вектором заменяется синусоидально распределенная н.с. Его проекция на линию, проведенную через центр внутренней окружности статора и любую ее точку, определяет н.с., соответствующую этой точке.

Пространственный вектор  или  при вращении опишет окружность, поэтому соответствующая н.с. называется круговой вращающейся н.с.

Определим значение -й гармоники н.с. для той же точки х (рис. 3-25). Оно равно:

,          (3-48)

так как теперь тому же сдвигу х относительно оси фазы А будет соответствовать сдвиг  в электрических радианах (полюсное деление для -й гармоники равно t/ν). Заменим пульсирующую н.с. F_txν двумя вращающимися:

.          (3-49)

Рассуждая аналогично предыдущему, найдем, что одна из них перемещается со скоростью  или вращается с частотой

,          (3-50)

в ν раз меньшей частотой вращения первой гармоники. Вторая н.с. вращается в обратную сторону с той же частотой:

.          (3-51)

Вверх

Глава 4