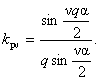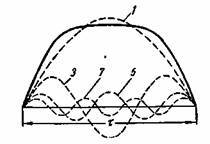
е) Электродвижущие силы при несинусоидальном поле.

 На рис. 3-21 представлена кривая поля (сплошная линия), созданного, например, вращающимися полюсами.

Рис. 3-21. Кривая поля и ее гармоники.

Ее можно разложить на гармоники, причем вследствие симметрии кривой относительно оси абсцисс и максимальной ординаты в разложении будут иметь место только синусоиды нечетного порядка, показанные на рис 3-21 пунктиром.

Все гармоники поля вращаются относительно статора с одной и той же частотой, равной частоте вращения полюсов. Полюсное деление первой или основной гармоники равно t, полюсное деление -й гармоники равно t/ν. Таким образом, ν-я гармоника поля имеет в ν раз больше полюсов, чем первая гармоника.

Электродвижущая сила, наведенная в фазе обмотки ν-й гармоникой поля, равна:

          (3-23)

где

          (3-24)

— частота v-й гармоники э.д.с., в ν раз большая, чем частота f₁ первой гармоники э.д.с.;

          (3-25)

— поток, соответствующий v-й гармонике поля;

          (3-26)

— обмоточный коэффициент для v-й гармоники э.д.с.

Обмоточный коэффициент k₀₁ для первой гармоники, очевидно, не отличается от k₀, рассмотренного нами ранее; k_0ν для высших гармоник отличается от k₀₁, так как сдвиг по фазе э.д.с. сторон витка и э.д.с. катушек, составляющих катушечную группу, зависит от номера гармоники v.

Сдвиг по фазе э.д.с. сторон витка, наведенных v-й гармоникой поля, равен vγ, где γ — сдвиг сторон витка в электрических градусах для первой гармоники поля; следовательно,

          (3-27)

Коэффициент распределения для v-й гармоники рассчитывается по формуле

          (3-28)

Значения k_уν и k_pv для гармоник э.д.с. приведены в табл. 3-1 и 3-2.

Таблица 3-1

 Таблица 3-2

 (Знаки перед значениями k_уν и k_pv учитываются при определении мгновенного значения результирующей э.д.с.)

Из табл. 3-1 следует, что путем выбора шага мы можем значительно уменьшить амплитуды высших гармоник в кривой фазной э.д.с.

Действующее значение фазной э.д.с.

.          (3-29)

Так как в обычных случаях амплитуды высших гармоник сравнительно с амплитудой первой гармоники невелики, мы можем практически считать:

          (3-30)

где f₁ и k₀₁ определяются для первой гармоники, а Ф (индекс «м» здесь и в последующем опускаем) — по первой гармонике кривой поля (или приближенно по действительной кривой поля).

Гармоники фазных э.д.с. трехфазной обмотки с номером, кратным трем, совпадают по фазе, прочие гармоники фазных э.д.с. (5, 7, 11, 13. 17, ...) той же обмотки будут сдвинуты по фазе на 120°.

Следовательно, при соединении обмотки звездой в линейной э.д.с. все гармоники с номером, кратным трем, пропадают:

.          (3-31)

При соединении обмотки треугольником мы также не будем иметь в линейном напряжении гармоник с номером, кратным трем, так как при таком соединении все эти гармоники по контуру, составленному из трех фаз об мотки, будут в любой момент времени направлены в одну и ту же сторону (фазы обмотки для гармоник с номером, кратным трем, могут рассматриваться как последовательно соединенные генераторы).

Вверх

Глава 4