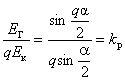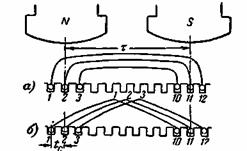
Обратимся к рис. 3-8,а и б, где изображены две катушечные группы трехфазной обмотки: одна состоит из различных по ширине катушек, другая — из катушек, одинаковых по ширине. Каждая катушка второй группы имеет ширину, равную t, поэтому э.д.с. катушки здесь получается в результате арифметического сложения э.д.с. ее сторон. Обозначим э.д.с. катушек через E_к1, E_к2, Е_к3. Они равны по величине, но по фазе сдвинуты на угол  В соответствии с этим построим диаграмму э.д.с. катушек группы, изображенной на рис. 3-8,б.

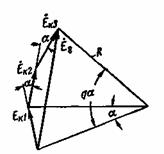
Рис. 3-8. Катушечные группы однослойной обмотки.

Рис. 3-9. Определение э.д.с. катушечной группы.

Диаграмма представлена на рис. 3-9. Она позволяет определить э.д.с. Е_г катушечной группы, которая в общем случае состоит из q катушек. Из диаграммы получаем:

          (3-16)

и э.д.с. катушки

          (3-17)

где R — радиус описанной окружности.

Отношение

          (318)

называется коэффициентом распределения. Он, следовательно, равен отношению геометрической суммы э.д.с. катушек катушечной группы к арифметической сумме тех же э.д.с. Учитывая (3-11) и (3-18), получим:

          (3-19)

Точно такую же э.д.с. мы получим и для катушечной группы рис. 3-8,а, соответствующей рис. 3-6, так как в нее входят те же катушечные стороны, что и в группу рис. 3-8,б. Следовательно, обмотка рис. 3-6 в отношении получения э.д.с. может рассматриваться как обмотка с одинаковыми катушками, имеющими ширину, равную t, т. е. как диаметральная.

В однослойной обмотке при 2р = 2 одну фазу составляет одна катушечная группа; при 2р > 2 фаза состоит из р катушечных групп, которые могут быть соединены последовательно, параллельно или последовательно-параллельно. Все р катушечных групп имеют одинаковое число катушек, равное q. Если на фазу взято а параллельных ветвей, то общее число последовательно соединенных витков фазы, определяющее ее э.д.с., равно:

          (3-20)

Следовательно, э.д.с. фазы обмотки

          (3-21)

где

          (3-22)

есть обмоточный коэффициент. Он равен, как это следует из предыдущего, отношению геометрической суммы э.д.с. последовательно соединенных проводников фазы к их арифметической сумме.

Сравнивая формулу (3-21) с формулой (2-5) [или (2-6)], по которой определяется э.д.с. в обмотке трансформатора, мы видим, что для трансформатора обмоточный коэффициент равен единице, так как э.д.с. во всех витках его обмотки совпадают по фазе.

Вверх

Глава 4