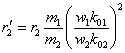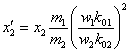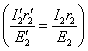Уравнения напряжений для фаз статора и ротора можем написать так же, как для первичной и вторичной обмоток трансформатора. Уравнение напряжений роторной цепи (3-85) после деления его членов на s получает следующий вид:

.          (3-88)

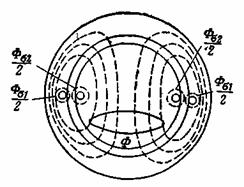
Отсюда также видим, что при замене вращающейся машины неподвижной, когда она работает как трансформатор (рис. 3-34), нужно в ее роторной цепи иметь активное сопротивление .

Рис. 3-34. Фазы обмоток статора и ротора асинхронной машины, работающей как трансформатор.

Тогда временной сдвиг н.с. статорной и роторной обмоток такого трансформатора будет соответствовать пространственному сдвигу н.с. вращающейся машины и мы можем написать:

;          (3-89)

здесь  взято с учетом потерь в стали статора P_с1, и вследствие этого несколько отличается от  на диаграмме рис. 3-31, где для упрощения мы пренебрегали этими потерями (практически ). Согласно (3-59) перепишем уравнение (3-89) в следующем виде:

.          (3-90)

Разделим обе части этого равенства на . При этом получим:

,          (3-91)

где

          (3-92)

есть ток ротора, приведенный к обмотке статора.

Обратимся теперь к уравнению напряжений роторной цепи (3-88). Помножим его на  и два последних члена правой части еще на.

Тогда, учитывая формулы для э.д.с. (3-77) и (3-80) и для приведенного тока (3-92), получим:

,          (3-93)

где          (3-94)

— э.д.с. обмотки ротора, приведенная к обмотке статора;

          (3-95)

и

          (3-96)

— сопротивления обмотки ротора, приведенные к обмотке статора.

С учетом (3-92) и (3-94) те же соотношения между r₂ и  и между х₂ и  мы получили бы, исходя из равенств:

 и ;          (3-97)

Приведенные величины  и  были бы равны действительным величинам обмотки ротора, если бы она была выполнена с теми же числами фаз, витков в фазе, пазов на полюс и фазу и с тем же шагом, что и обмотка статора. В такой обмотке электрические потери, а также относительные падения напряжения согласно (3-97) должны остаться неизменными.

Вверх

Глава 4