Кривая поля созданного н.с. F_в, строятся следующим образом.

Сначала определяется поток индукционной трубки имеющей длину по оси машины, равную 1 см:

.          (4-14)

Индукция в основании трубки

,          (4-15)

где  — магнитная проводимость индукционной трубки, имеющей ширину и длину основания, равные 1 см.

Кривая  при другом масштабе может рассматриваться, следовательно, как кривая распределения проводимости воздушного зазора вдоль внутренней окружности статора: λ_x = f(x).

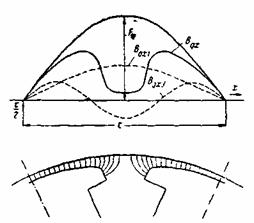
Мы будем считать, что форма кривой B_вх = f(x) не зависит от насыщения зубцов и ярма статора, что близко к действительным условиям, так как синхронные машины обычно имеют относительно большие воздушные зазоры.

Кривую поля B_dx = f(x), созданного продольной н.с. якоря, найдем по соотношению

,          (4-16)

так как продольная н.с. якоря по его окружности распределена синусоидально.

Если бы нам удалось так подобрать F_d и F_в, чтобы амплитуды первых гармоник (пунктирная синусоида на рис 4 19,а) кривых В_вх = f(x) и B_dx = f(x) были равны, то F_d и F_в были бы эквивалентны по индуктирующему действию и . Практически для определения k_d можно построить кривые полей В_вх и B_dx при F_d = F_в. Тогда отношение амплитуд первых гармоник соответствующих кривых полей будет равно k_d.

Кривая поля В = f(х), созданного поперечной н.с. якоря F_q, показана на рис. 4-20.

Рис. 4-20. Поперечное поле (к определению k_q).

Она находится аналогичным образом по картине поля. Если взять F_q = F_в, то отношение амплитуд первых гармоник кривой В_ax = f(x) и кривой B_вx = f(x) (рис. 4-19,а) будет равно k_q.

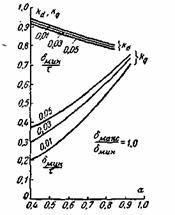
На рис. 4-21 и 4-22 приведены значения k_d и k_q в зависимости от коэффициента полюсного перекрытия  для различных отношений  при равномерном воздушном зазоре и при  =1,5 (размеры b_р, δ_мин, δ_макс, τ указаны на рис. 4-19).

Рис. 4-21. Кривые k_d = f(α) и k_q = f(α.) для различных значений  при равномерном воздушном зазоре.

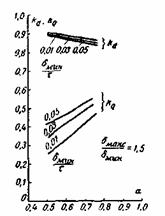
Рис. 4-22. Кривые k_d = f(α) и k_q = f(α.) для различных значений  при .

Для машин примерно до 100 кВА часто берут равномерный зазор, для машин большей мощности обычно  =1,5.

Вверх

Глава 5