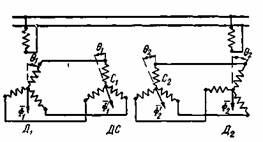
Если теперь повернуть ротор сельсина СД на некоторый угол θ, то токи в фазах обмоток С_Д  и С_П изменяются и ось н.с. обмотки С_П также повернется на угол θ. При этом на зажимах обмотки В_П возникнет напряжение, зависящее от угла θ. Оно непосредственно воздействует на усилитель У, выход которого соединен с исполнительным двигателем ИД. Двигатель ИД приводит в действие нагрузку и одновременно поворачивает ротор СТ в такое положение, при котором ось н.с. его обмотки С_П  снова будет сдвинута на 90° относительно оси обмотки В_П. Таким образом, нагрузочный механизм будет повторять повороты или вращение ротора СД. Исполнительный механизм и датчик СД не нуждаются в механической связи и могут быть расположены на большом расстоянии один от другого, причем линия связи Л здесь не требует больших затрат, так как передаваемая ею мощность (в соответствии с мощностью СД и СТ) весьма мала.

Если необходимо осуществить управление из двух пунктов, применяется дифференциальный сельсин. В отличие от ранее рассмотренных сельсинов он имеет на роторе и на статоре трехфазные обмотки и используется обычно в качестве приемника, а в качестве датчиков для него служат два однофазных сельсина (рис. 3-118).

Рис. 3-118. Схема управления дифференциальным сельсином-приемником ДС при помощи двух обычных сельсинов-датчиков Д₁ и Д₂.

Работа дифференциального сельсина протекает следующим образом.

Предположим, что ротор датчика D₁ совершил поворот по часовой стрелке на угол θ₁. При этом ось н.с. обмотки С₁ и создаваемого ею потока  также повернется на угол θ₁, но против часовой стрелки. Поворачивая ротор датчика D₂ по часовой стрелке на угол θ₂, получим поворот оси н.с. обмотки С₂ и создаваемого ею потока  на тот же угол θ₂, но также против часовой стрелки. Создается вращающий момент, действующий таким образом, чтобы магнитные потоки  и  совпали по направлению. Следовательно, ротор дифференциального сельсина должен повернуться на угол θ₂ - θ₁. Если ротор датчика D₂ повернут на угол θ₂ против часовой стрелки, то ротор дифференциального сельсина поворачивается на угол, равный сумме углов θ₁ - θ₂.

Вверх

Глава 4