Теперь уравнения напряжений для первичной обмотки напишутся следующим образом:

          (2-156)

Заменим

          (2-157)

где Z₀ = r₀ + jx₀ — полное сопротивление нулевой последовательности (x₀ обусловлено полем тока I_a0, а r₀ — магнитными потерями от этого поля).

Сложив уравнения (2-156) и, учитывая при этом (2-155), (2-148) и (2-157), получим:

          (2-158)

Для линейных (междуфазных) напряжений можем написать:

          (2-159)

Отсюда с учетом (2-158) получим:

          (2-160)

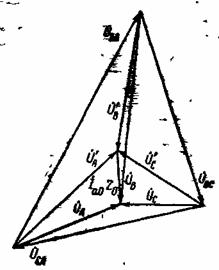
В соответствии с (2-160) на рис. 2-63 построена векторная диаграмма первичных напряжений.

Рис. 2-63. Векторная диаграмма первичных напряжений.

 Из нее мы видим, что вследствие наличия токов нулевой последовательности потенциал нулевой точки первичной обмотки сместился на величину  из центра тяжести треугольника линейных напряжений.

Учитывая (2-160) в (2-154) напишем уравнения напряжений для вторичной обмотки:

или, так как  и , а

          (2-161)

где

_.          (2-162)

Для двух других фаз уравнения напряжений напишутся аналогично:

          (2-163)

          (2-164)

Уравнения (2-161), (2-163) и (2-164) показывают, что смещение потенциала нулевой точки вторичной обмотки, вызванное токами нулевой последовательности, равно . Оно несколько больше, чем для первичной обмотки, где это смещение равняется . Оба сопротивления Z₀ и Z_н называются сопротивлениями нулевой последовательности; они практически мало отличаются одно от другого. Для трехфазных стержневых трансформаторов с масляным охлаждением

          (2-165)

Вверх

Глава 3