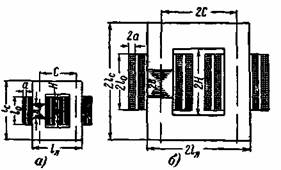
Мощность, потери и размеры трансформаторов связаны важными практически соотношениями, имеющими общее значение и для всех электрических машин.

Представим себе ряд трансформаторов возрастающей мощности, геометрически подобных друг другу и имеющих одинаковые плотности тока D (A/мм²) в обмотках и одинаковые индукции В (Гс) в сердечниках. Под геометрически подобными трансформаторами понимаются трансформаторы, соответственные размеры которых находятся в одном и том же отношении. Два геометрически подобных трансформатора изображены на рис. 2-80.

Рис. 2-80. Геометрически подобные трансформаторы.

 Здесь все линейные размеры второго трансформатора в 2 раза больше соответственных линейных размеров первого трансформатора.

Мощность трансформатора пропорциональна произведению э.д.с. и тока, т. е.

          (2-189)

При данной частоте тока э.д.с. Е пропорциональна числу витков w обмотки и магнитному потоку Ф:

E º wФ.          (2-190)

Заменяя Ф = BS_c, где В — индукция в сечении S_с, получим:

E º wBS_c.          (2-191)

Ток I = Ds_n, где D — плотность тока в проводнике, имеющем сечение s_n. Поэтому вместо (2-189) можем написать:

P º wBS_cDs_n.          (2-192)

Если обозначить общее сечение меди всех витков обмотки через S_м = ws_n, то получим:

P º BDS_cS_м.          (2-193)

Площади S_c и S_м пропорциональны квадрату линейного размера, причем здесь мы можем взять любой линейный размер (рис. 2-80), который обозначим через l; следовательно,

S_cS_м º l²l² = l⁴.          (2-194)

Вместо (2-193) мы можем теперь написать (при D = const и В = const):

P º l⁴          (2-195)

или

l º P^1/4.          (2-196)

Веса активных материалов (стали и меди) пропорциональны их объему, т. е. кубу линейных размеров:

G º l³,          (2-197)

поэтому

G º P^3/4.          (2-198)

Следовательно, вес трансформатора при увеличении линейных размеров растет медленнее, чем его мощность.

Можно считать, что стоимость С активных материалов и потери SP в них при заданных индукции и плотности тока также пропорциональны весу:

C º G º P^3/4;          (2-199)

SP º G  º l³ º P^3/4.          (2-200)

Если отнести вес, стоимость трансформатора и его потери к единице мощности, то получим:

          (2-201)

Следовательно, вес и стоимость активных материалов на 1 кВА и относительное значение потерь (потерь на единицу мощности) в ряде геометрически подобных трансформаторов изменяются обратно пропорционально корню четвертой степени из их мощности при сохранении постоянными значений D и В.

Этим и объясняется тенденция применять в современных электроустановках (там, где это возможно и целесообразно) трансформаторы большой мощности вместо нескольких малых трансформаторов той же суммарной мощности.

Из равенства (2-200) следует, что потери трансформатора растут пропорционально кубу линейных размеров. Но его поверхность охлаждения возрастает пропорционально только квадрату линейных размеров. Поэтому по мере увеличения мощности трансформаторов приходится повышать интенсивность их охлаждения и отступать от геометрического подобия их форм.

Приведенные соотношения (2-198) (2-201) дают лишь общую ориентировку при определении зависимости мощности трансформатора и его потерь от размеров, и они правильны лишь приближенно. При проектировании ряда трансформаторов возрастающей мощности приходится в той или иной мере от них отступать по конструктивным, технологическим и прочим соображениям.

Вверх

Глава 3