Расчет активных сопротивлений r_j и r_2, Ом, может быть произведен, если известны сечения проводников обмоток s₁ и s₂, мм², число витков w_l и  w₂ и средние длины  витков l_ср1 и l_ср2, м. Тогда имеем:

где k_r = 1,03  1,05 — коэффициент, учитывающий потери, вызванные полями рассеяния обмоток;

 — удельное сопротивление меди при 75° С;

 — тоже для алюминия.

Активное сопротивление короткого замыкания

Потери в обмотках при номинальных токах (сюда же относятся и потери, вызванные полями рассеяния), Вт

Формулы для потерь можно преобразовать следующим образом:

подставив  ─ квадрат плотности тока первичной обмотки, А/мм²;   ─ удельный вес меди;  ─ вес меди первичной обмотки, кг, получим:

          (2-69)

аналогично будем иметь.

          (2-70)

при алюминиевых обмотках (γ_а  2,65)

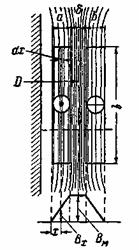
где G_al и G_a2 — веса обмоток, кг.

Расчет индуктивных сопротивлений рассеяния х₁ и х₂ может быть произведен только приближенно, так как не представляется возможным точно установить распределение поля рассеяния. Мы рассмотрим метод расчета х₁ и х₂ для цилиндрических обмоток. Они в разрезе с одной стороны стержня показаны на рис. 2-47. Здесь же показана часть стержня, на котором помещены обмотки.

Рис. 2-47. К расчету х_к = х₁ + х'₂ (см. рис. 2-13).

 Мы считаем, что поле рассеяния создается н.с. i₁w₁ и равной ей н.с. i₂w₂ =  (пренебрегаем при этом н.с. i₀w₁) и что индукционные линии этого поля направлены, как показано на рис. 2-47, параллельно стенкам обмоток, равным по высоте. Примем, что магнитные сопротивления индукционных трубок поля обусловлены только их частью вдоль обмоток и промежутка между ними. Магнитным сопротивлением остальных частей индукционных трубок пренебрегаем. Кривая н.с., создающей поле рассеяния, в этом случае изобразится трапецией, а так как μ для воздуха (или масла), меди и изоляции — величина постоянная, то кривая распределения индукции вдоль пунктирной линии также изобразится трапецией.

Вверх

Глава 3