а) Метод симметричных составляющих.

 Мы здесь сообщим краткие сведения о методе симметричных составляющих. Сущность этого метода состоит в том, что каждый фазный ток (или фазное напряжение) заменяется тремя его составляющими:

          (2-135)

          (2-136)

          (2-137)

Величины  принимаются равными друг другу и равными одной трети суммы фазных токов:

          (2-138)

Эти величины называются составляющими нулевой последовательности, так как они образуют три равных временных вектора с нулевым сдвигом между ними.

Если из каждого тока данной несимметричной системы вычесть его нулевую составляющую, то получим новую систему токов, сумма которых согласно (2-138) равна нулю:

          (2-139)

Учитывая теперь (2-135) — (2-137), можем написать:

          (2-140)

Здесь системы токов, стоящих в скобках, будем считать трехфазными симметричным системами. Однако, если принять, что порядки чередования фаз той и другой систем одинаковы, то   их сумма даст симметричную систему, что в общем случае не будет соответствовать системе токов уравнения (2-139). Следовательно, мы должны считать, что одна из систем токов (2-140) имеет порядок чередования фаз, обратный по отношению к порядку чередования фаз     другой. В соответствии с этим система токов  называется системой прямой последовательности [порядок чередования этих токов обычно такой же, как и токов уравнения (2-139)], а система токов  — системой обратной последовательности.

Для удобства вычислений вводится комплексный коэффициент

          (2-141)

Умножение вектора на этот коэффициент не изменяет его абсолютного значения, но изменяет его аргумент на  т. е. поворачивает  вектор на угол  в сторону вращения векторов. Очевидно, что умножение на а² дает поворот вектора на угол  в ту же сторону. Также очевидно, что

            (2-142)

Уравнения (2-135) — (2-137) после введения в них коэффициентов а и а² и с учетом (2-138) перепишем в следующем виде

          (2-143)

          (2-144)

          (2-145)

Написанные уравнения позволяют при заданных токах найти их симметричные составляющие. Составляющие нулевой последовательности  определяются по (2-138). Составляющие прямой и обратной последовательно­стей определяются следующим образом.

Умножим (2-144) на а и (2-145) на а². Сложив полученные уравнения с (2-143) и учитывая (2-142), будем иметь:

          (2-146)

Если умножить (2-144) на а² и (2-145) на а, то, сложив три уравнения, получим:

          (2-147)

Таким образом, по (2-138), (2-146) и (2-147) при заданных токах  могут быть определены их симметричные составляющие (на рис 2-58 показаны токи  и их симметричные составляющие).

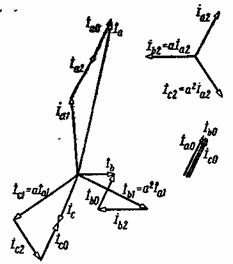
Рис. 2-58. Несимметричная система таков  и их симметричные составляющие.

 Аналогичные уравнения получаются для симметричных составляющих заданной системы напряжений  Фазные токи или напряжения в общем случае имеют составляющие всех трех последовательностей: линейные токи (при соединении треугольником) и напряжения могут иметь только составляющие прямой и обратной последовательностей.

В обычных случаях системы симметричных составляющих токов или напряжений можно рассматривать независимо одна от другой и при исследовании несимметричной нагрузки исходить из принципа наложения. Если, например, трехфазная система сопротивлений симметрична, то можно считать, что токи любой последовательности вызовут падения напряжения — активные и реактивные — только той же самой последовательности. В применении к трехфазным трансформаторам мы должны считать Z₁₂= const, т. е пренебречь изменением насыщения, или считать Z₁₂ = ∞, т е. пренебречь током холостого хода.

Вверх

Глава 3