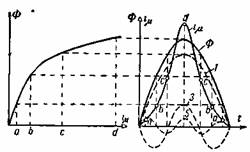
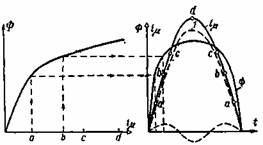
Рассмотрим вначале процесс намагничивания однофазного трансформатора. Как отмечалось, вследствие нелинейной связи между потоком Ф в стальном сердечнике трансформатора и создающей его н.с. i₀w₁ кривая i₀ = f(t) отличается от синусоиды. Мы эту кривую найдем, пренебрегая потерями в стали и рассматривая вместо тока i_o намагничивающий ток i_μ, прак­тически равный i₀.

Кривую Ф = f(t) можно принять синусоидальной, если приложенное напряжение u₁ и, следовательно, уравновешивающая его э.д.с. е₁ — синусоидальные функции времени. В этом случае кривая i_μ = f(t) определяется графически, как показано на рис. 2-41.

Рис. 2-41. Построение кривой намагничивающего тока i_μ = f(t) однофазного трансформатора при синусоидальном потоке.

 Слева мы имеем кривую намагничивания Ф = f(i_μ) (здесь пренебрегаем гистерезисом). Справа для заданной синусоидальной кривой Ф = /(t) мы получаем кривую i_μ = f(t), ординаты которой a, b, с, d и т. д. равны абсциссам кривой Ф = f(i_μ) для соответствующих значений потока Ф.

Мы видим, что кривая тока искажена. Она имеет наряду с первой гармоникой довольно резко выраженные третью и пятую гармоники. Кривая тока построена для нормального трансформатора, имеющего, как это обычно бывает, максимальную индукцию в сердечнике около 14 500 Гс. В этом случае гармоники с номером выше пятого имеют небольшие значения.

Гистерезис мало искажает кривую тока. При разложении на гармоники кривой тока, построенной с учетом гистерезиса, мы получили бы, кроме синусоид, еще косинусоиды с малыми амплитудами. Они дают активную составляющую тока i_о, соответствующую потерям от гистерезиса.

При некоторых схемах соединения обмоток трехфазного трансформатора в кривой намагничивающего тока отсутствуют третья гармоника и гармоники с номером, кратным трем. Если принять кривую i_μ = f(t) синусоидальной, то кривая Ф = /(t) будет отличаться от синусоиды. Из высших гармоник в ней наиболее резко будет выражена 3-я гармоника. На рис. 2-42 приведено построение кривой Ф = /(t) при синусоидальной кривой i_μ = f(t).

Рис. 2-42. Построение кривой Ф = /(t) при синусоидальном намагничивающем токе.

 Здесь по абсциссам а, b, с и т. д., равным ординатам кривой i_μ = f(t), найдены соответствующие значения потока Ф.

Вверх

Глава 3