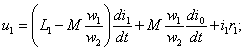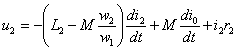б) Уравнения напряжений.

 Будем вначале считать, что потокосцепления обмоток трансформатора пропорциональны их токам и что магнитные потери в сердечнике отсутствуют (такие условия получаются в воздушном трансформаторе). При этом, так же как для двух магнитно связанных контуров, можем написать следующие уравнения напряжений первичной и вторичной обмоток трансформатора:

;          (2-20)

,          (2-21)

где u₁ и u₂ — мгновенные значения первичного и вторичного напряжений;
L₁, L₂ и М — полные индуктивности и взаимная индуктивность обмоток;
r₁ и r₂ — их активные сопротивления.

Первичное напряжение u₁ имеет составляющие, уравновешивающие э.д.с. cамоиндукции  и взаимоиндукции , и составляющую, равную активному падению напряжения i₁r₁. Вторичное напряжение u₂ получается после вычитания из результирующей э.д.с. самоиндукции и взаимоиндукции  активного падения напряжения i₂r₂.

Полагая, так же как и в предыдущем, что в сердечнике трансформатора имеет место главный поток Ф, который создается результирующей н.с. i₀w₁ мы можем для токов i₁, и i₂ согласно (2-14) написать следующие равенства:

          (2-22)

          (2-23)

Подставив (2-23) в (2-20) и (2-22) в (2-21), получим:

          (2-24)

          (2-25)

или

          (2-24a)

          (2-25a)

где  и — индуктивности рассеяния первичной и вторичной обмоток; им соответствуют э.д.с. рассеяния:

;          (2-26)

          (2-27)

Электродвижущие силы

          (2-28)

          (2-29)

рассматриваются как э.д.с., наведенные главным потоком Ф.

Приведем здесь уравнения, относящиеся к общей теории двух магнитно связанных обмоток. Для потокосцеплении этих обмоток можем написать:

          (2-30)

          (2-31)

Вычтем и прибавим с правой стороны написанных равенств одни и те же величины:

Здесь коэффициенты  и имеют произвольные значения.

Будем называть величины

 и  

главными потокосцеплениями обмоток, а величины

 и  

их потокосцеплениями рассеяния.

Главными индуктивностями обмоток назовем величины

Общий коэффициент рассеяния равен:

          (2-32)

Коэффициенты рассеяния обмоток равны отношениям индуктивностей рассеяния к главным индуктивностям:

 и .          (2-33)

Вверх

Глава 3