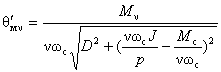б) Колебания ротора под действием периодически изменяющегося момента на его валу.

 Найдем изменение углового отклонения , вызванного n-й гармоникой избыточного момента. Для этого уравнение (4-100) напишем в следующем виде:

.          (4-101)

Решением этого уравнения при установившихся колебаниях будет синусоидальная функция времени, которую мы можем представить в виде временного вектора

.          (4-102)

где  — амплитуда углового отклонения, вызванного ν-й гармоникой избыточного момента М_ν;

φ_ν — сдвиг по фазе М_ν и .

Следовательно, уравнение (4-101) можно написать в векторной форме:

          (4-103)

или соответственно

.          (4-104)

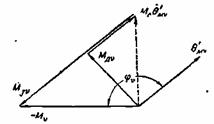
Согласно (4-104) и (4-103) на рис. 4-93 построена векторная диаграмма моментов. (Пунктирный вектор — есть вектор мощности, колеблющейся с частотой νω_c. Амплитуда этой мощности равна: .)

Рис. 4-93. Векторная диаграмма моментов.

Из нее находим амплитуду углового отклонения

.          (4-105)

Если частота νω_с колебания ν-й гармоники удовлетворяет равенству

,          (4-106)

то амплитуда  может достичь весьма большого значения, особенно при малом D:

.          (4-107)

Частота колебаний, найденная из (4-106),

          (4-108)

есть так называемая резонансная частота.

Частоту собственных колебаний найдем из уравнения (4-101), приравняв его правую часть нулю

.          (4-109)

Разделим это уравнение на  и введем обозначения:

;          (4-110)

.          (4-111)

Тогда оно будет иметь следующий вид:

.          (4-112)

Решением этого уравнения, как известно, будет:

,          (4-113)

где  — начальное отклонение;

δ₀ — коэффициент затухания;

ω_св — частота собственных или свободных колебаний, равная

.          (4-114)

так как  во много раз меньше .

Сравнивая выражения для частоты собственных колебаний (4-114) и для резонансной частоты (4-108), мы видим, что они практически равны между собой. Поэтому мы можем говорить, что резонанс наступает в том случае, когда частота вынужденных колебаний равна частоте собственных колебании.

Вверх

Глава 5