|
Заменим в (45) локальные переменные
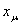 и и
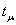 соответственно на х и
t, а пульсирующие, другими
словами, с фиксированными в пространстве узловыми точками,
пространственные гармонические волны МДС эквивалентной им суммой
двух встречно вращающихся пространственных волн с тем же
пространственным периодом и уменьшенной вдвое и Неизменной во
времени амплитудой. Расчетное выражение для искомой МДС
F(x,
t) приобретет следующий вид: соответственно на х и
t, а пульсирующие, другими
словами, с фиксированными в пространстве узловыми точками,
пространственные гармонические волны МДС эквивалентной им суммой
двух встречно вращающихся пространственных волн с тем же
пространственным периодом и уменьшенной вдвое и Неизменной во
времени амплитудой. Расчетное выражение для искомой МДС
F(x,
t) приобретет следующий вид:
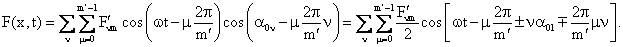
(50)
Условимся в дальнейшем под
значением порядка гармонической МДС ν понимать алгебраическую
величину, полагая ν > 0 для прямовращающихся волн МДС; ν <0 —
для обратно-вращающихся волн МДС. С учетом последнего замечания
уравнение (50) можно несколько упростить:
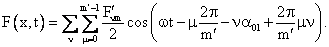 (51) (51)
Анализируя полученное соотношение
для МДС F(x,
t), замечаем, что отдельные
простейшие фазы действуют совместно и в одинаковой мере вносят
свой вклад в создание отдельных гармонических МДС. А именно это
имеет место по отношению к тем гармоническим, значение порядка
которых удовлетворяет соотношению
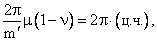 (52)
(52)
где ц. ч. =
0; ±1; ±2; ±3 и т. д.
|