|
Пространственные
основная х и локальные переменные
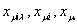 связаны между собой, как показывает анализ,
следующими соотношениями (см. рис. 2.3): связаны между собой, как показывает анализ,
следующими соотношениями (см. рис. 2.3):
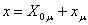 (28)
(28)
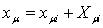 (29)
(29)
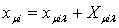 (30)
(30)
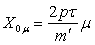 (31)
(31)
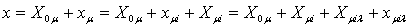 (32) (32)
где координата 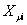 в фазной системе координат (для «µ»-й фазы)
«нуля» для переменной в фазной системе координат (для «µ»-й фазы)
«нуля» для переменной
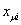 определяется из уравнения определяется из уравнения
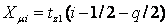 ,
(33) ,
(33)
а координата 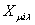 в катушечной системе координат (для «1»-й
катушки «µ»-й фазы) «нуля» для переменной в катушечной системе координат (для «1»-й
катушки «µ»-й фазы) «нуля» для переменной
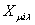 определяется из уравнения определяется из уравнения
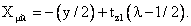 (34)
(34)
От линейных
координат несложно перейти к угловым (в эл. рад.):
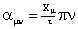 (35)
(35)
На основании
сказанного выше и рис. 2.4 нетрудно также установить соотношение
между угловой координатой
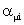 точки наблюдения в системе координат «µ»-й
простейшей фазы с угловой координатой той же точки наблюдения по
«ν»-й гармонической в осях основной «0»-й фазы. точки наблюдения в системе координат «µ»-й
простейшей фазы с угловой координатой той же точки наблюдения по
«ν»-й гармонической в осях основной «0»-й фазы.
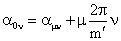 36)
36)
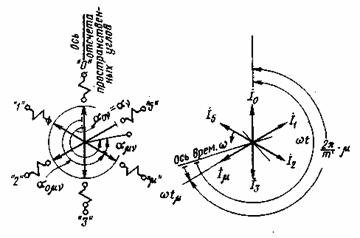
Рис. 2.4
|