|
С учетом (39) ряд Фурье для искомой
функции МДС многофазной обмотки можно представить в следующем
виде:
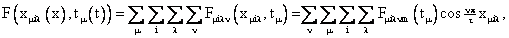 (40) (40)
откуда
видно, что результирующая МДС многофазной обмотки может быть
представлена в виде суперпозиции пульсирующих (с изменяющейся во
времени амплитудой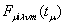 пространственных гармонических « пространственных гармонических «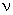 »-гo порядка,
соответствующих всевозможным элементарным МДС той же обмотки. »-гo порядка,
соответствующих всевозможным элементарным МДС той же обмотки.
Заменив в (40) локальную переменную
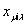 другой другой
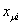 расчетному
выражению для МДС
F(x,
t)
можно придать следующий вид: расчетному
выражению для МДС
F(x,
t)
можно придать следующий вид:
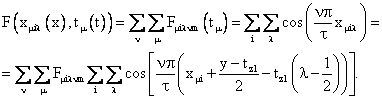 (41) (41)
Произведя суммирование
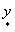 пространственных волн МДС «ν»-гo
порядка, входящих в состав ряда Фурье частичной (неполной иначе)
МДС обмотки, когда возбуждена только одна «i»-я
катушка «µ»-й простейшей фазы, получим пространственных волн МДС «ν»-гo
порядка, входящих в состав ряда Фурье частичной (неполной иначе)
МДС обмотки, когда возбуждена только одна «i»-я
катушка «µ»-й простейшей фазы, получим
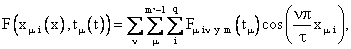 (42) (42)
где
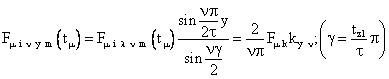 (43) (43)
амплитуда «ν»-ой
гармонической упомянутой выше частичной МДС, а коэффициент
укорочения для «ν»-ой гармонической.
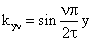 (44)
(44)
Заменим далее в (42) локальную
переменную 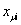 другой другой
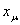 и произведем суммирование
q пространственных волн МДС «ν»-гo
порядка, входящих в состав ряда Фурье особой МДС обмотки, когда
возбуждена одна «µ»-я простейшая фаза, которая в пределах одного
двойного полюсного деления формируется из
q смещенных относительно друг друга на одно полюсное
деление катушек. Получим в итоге и произведем суммирование
q пространственных волн МДС «ν»-гo
порядка, входящих в состав ряда Фурье особой МДС обмотки, когда
возбуждена одна «µ»-я простейшая фаза, которая в пределах одного
двойного полюсного деления формируется из
q смещенных относительно друг друга на одно полюсное
деление катушек. Получим в итоге
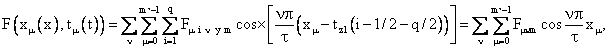
(45)
где
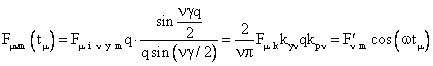 (46) (46)
изменяющаяся по гармоническому закону во времени амплитуда
«µ»-ой пространственной гармонической неполной МДС обмотки,
когда возбуждена только одна «µ»-я простейшая фаза;
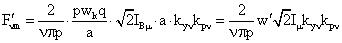 (47) (47)
максимальное значение амплитуды пульсирующей пространственной
«ν»
- ой
гармонической упомянутой выше неполной МДС обмотки, когда ток
простейшей фазы 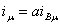 имеет максимальное положительное значение, т.
е. когда имеет максимальное положительное значение, т.
е. когда 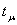 =0; =0;
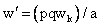 (48)
(48)
число
витков в простейшей фазе;
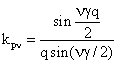 (49)
(49)
коэффициент распределения для «ν»-ой
гармонической.
|