|
Как следует из
вышеизложенного, МДС
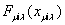 возбужденного « возбужденного «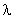 »-го зубцового контура, являющегося одним из »-го зубцового контура, являющегося одним из
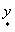 зубцовых контуров, на которые распадается «i»-я
катушка катушечной группы, представляющей на рассматриваемом
двойном полюсном делении «µ»-ю простейшую фазу, может быть
записана в форме следующего уравнения: зубцовых контуров, на которые распадается «i»-я
катушка катушечной группы, представляющей на рассматриваемом
двойном полюсном делении «µ»-ю простейшую фазу, может быть
записана в форме следующего уравнения:
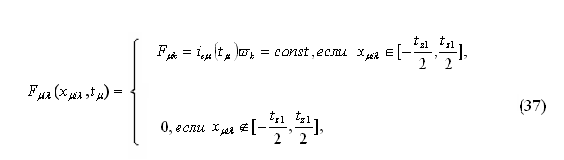
Результирующая
зависимость МДС многофазной целой обмотки определится из
уравнения
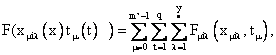 (38)
(38)
где 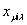 и и
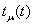 смотри соответственно в (32) и (27). При
замене полученной зависимости F(x,
t) эквивалентным рядом Фурье
удобно разлагать каждый из прямоугольных импульсов смотри соответственно в (32) и (27). При
замене полученной зависимости F(x,
t) эквивалентным рядом Фурье
удобно разлагать каждый из прямоугольных импульсов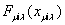 вначале в локальной пространственной системе
координат для данного момента времени вначале в локальной пространственной системе
координат для данного момента времени
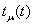 , а затем, используя соотношения (28)—(32),
переходить к основной пространственной координате х.
Преимущество такого подхода состоит в том, что гармонический ряд
Фурье для каждого прямоугольного импульса МДС зубцовых контуров , а затем, используя соотношения (28)—(32),
переходить к основной пространственной координате х.
Преимущество такого подхода состоит в том, что гармонический ряд
Фурье для каждого прямоугольного импульса МДС зубцовых контуров
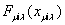 содержит только четные гармонические, а их
амплитуды содержит только четные гармонические, а их
амплитуды
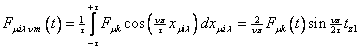 , (39) , (39)
как и следовало ожидать, не зависят от индексов
i,
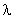 , а определяются переменной во времени высотой , а определяются переменной во времени высотой
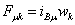 прямоугольного импульса МДС многофазной
обмотки при условии когда возбужден только один «λ»-й зубцовый
контур «i»-й катушки «μ»-й
простейшей фазы током ее ветви прямоугольного импульса МДС многофазной
обмотки при условии когда возбужден только один «λ»-й зубцовый
контур «i»-й катушки «μ»-й
простейшей фазы током ее ветви
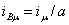 (a — число
параллельных ветвей простейшей фазы); относительной шириной
зубцового деления (a — число
параллельных ветвей простейшей фазы); относительной шириной
зубцового деления 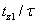 и порядком гармонической и порядком гармонической
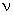 . Результирующая МДС многофазной обмотки
F(x,
t) в соответствии с (38) представляет
собой сумму элементарных МДС той же обмотки . Результирующая МДС многофазной обмотки
F(x,
t) в соответствии с (38) представляет
собой сумму элементарных МДС той же обмотки
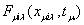 , определяемых при условии протекания тока
ветви одной из простейших фаз , определяемых при условии протекания тока
ветви одной из простейших фаз
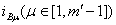 только в одном « только в одном «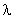 »-м »-м
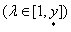 зубцовом контуре, входящем в состав «i»-й
катушки зубцовом контуре, входящем в состав «i»-й
катушки 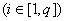 « «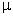 »-й простейшей фазы и равенстве нулю токов
ветвей во всех прочих простейших фазах. Нетрудно понять, что
в этом случае все члены тройной суммы в (38) обращаются в нуль,
кроме одного. »-й простейшей фазы и равенстве нулю токов
ветвей во всех прочих простейших фазах. Нетрудно понять, что
в этом случае все члены тройной суммы в (38) обращаются в нуль,
кроме одного.
|





 |