2.2. Решение задачи с использованием модели,
представленной на рис. 2.2
Считаем, что в
зазоре 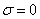 ; ;
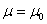 ;
сторонние (возбуждающие) токи отсутствуют, т.е. ;
сторонние (возбуждающие) токи отсутствуют, т.е.
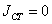 ; ;
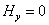 ;
Hx и Hz
от координаты у не зависят. ;
Hx и Hz
от координаты у не зависят.
С учетом этих допущений уравнения (1.29) приобретают вид
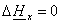
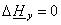 (2.3) (2.3)
Раскрывая оператор набла, имеем:
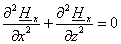 ; ;
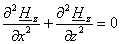 (2.4) (2.4)
Решение этой системы уравнений определит характер
магнитного поля идеального индуктора.
Токовые слои на поверхностях индукторов образуют бегущие
волны I (условие задачи). Поэтому магнитное поле тоже должно быть бегущим
и синусоидальным. Решение системы (2.4) можно искать в виде:
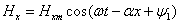
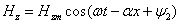
или в комплексной форме
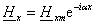
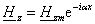 (2.5) (2.5)
Подстановка (2.5) в (2.4) дает (после сокращения на
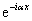 ): ):
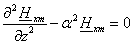 (2.6) (2.6)
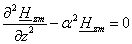
Решения этих уравнений имеют вид:
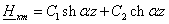
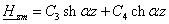 (2.7) (2.7)
где C1,
C2, С3, С4—постоянные
интегрирования, подлежащие определению на основании граничных условий. В общем
случае плотности токового слоя на верхнем и нижнем магнитопроводе индуктора
могут быть записаны в виде:
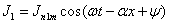
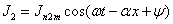
или в комплексном виде:
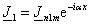 (2.8) (2.8)
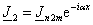
Из рис.2.4 и на основании закона полного тока
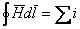 (2.9) (2.9)
следует, что тангенциальные
составляющие вектора 3, т. е. Нх на границах
равны:
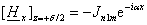 (2.10) (2.10)
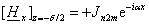
Граничные условия для нормальных составляющих
Hz можно получить на основе уравнения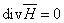 ,
или в рассматриваемой модели ,
или в рассматриваемой модели
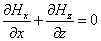
С помощью (2.10) имеем:
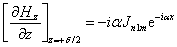 (2.11) (2.11)
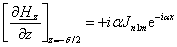
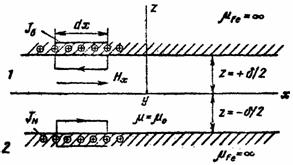
Рис. 2.4.
Опуская процесс
последовательного определения постоянных C1, С2,
С3, С4 получаем в окончательном (виде выражения
для комплексных амплитуд составляющих магнитного поля
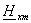 и и
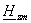 : :
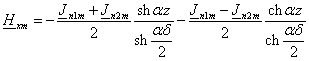 (2.12)
(2.12)
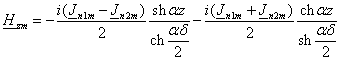 (2.13) (2.13)
Если считать обмотки обеих индукторов одинаковыми, т.е.
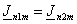 и
ввести обычное в теории электрических машин понятие линейной токовой нагрузки и
ввести обычное в теории электрических машин понятие линейной токовой нагрузки
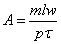 ,
где т — число фаз, w — число
последовательных витков фазы, l
— действующее значение тока, р — число пар полюсов, τ —
полюсное деление, выражения (2.1) и (2.3) могут быть выражены через МДС обмотки. ,
где т — число фаз, w — число
последовательных витков фазы, l
— действующее значение тока, р — число пар полюсов, τ —
полюсное деление, выражения (2.1) и (2.3) могут быть выражены через МДС обмотки.
Пусть обмотки обеих индукторов образуют одну единую
обмотку, ток I —
полный ток фазы при последовательном соединении обмоток, a
w — полное число витков всего индуктора.
Тогда амплитуду волны МДС можно записать как
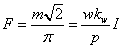 (2.14)
(2.14)
где kw—обмоточный
коэффициент (основной гармоники). Выражая ток I
через линейную нагрузку А имеем
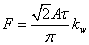 (2.15) (2.15)
Волна поверхностного тока должна иметь выражение
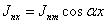 (2.16) (2.16)
а кривая МДС
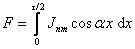 (2.17) (2.17)
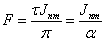 (2.18) (2.18)
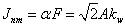 (2.19) (2.19)
Кривые поверхностного тока и МДС доказаны на рис. 2.5.
Теперь считая
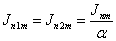 ,
окончательно имеем: ,
окончательно имеем:
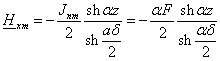 (2.20) (2.20)
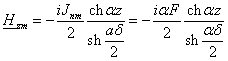
Кривые для Нхт и Нzт
по высоте зазора показаны на рис. 2.6.
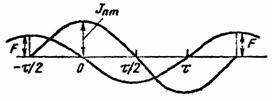
Рис. 2.5.
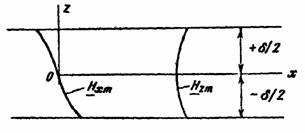
Рис. 2.6.
Составляющая Нхт в центре зазора
обращается в ноль, а нормальная составляющая Нzт
ослабляется. Степень ослабления нормальной составляющей можно определить как
отношение Нzт на поверхности
индуктора к его значению в центре зазора
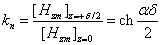 (2.21) (2.21)
При больших немагнитных зазорах
δ ослабление поля значительно. Например, при δ/τ около 0,7
значение коэффициента ослабления kn=1,7.
|
