2.5. Решение задачи для индуктора конечной длины
Расчетная модель индуктора показана на рис. 2.12.
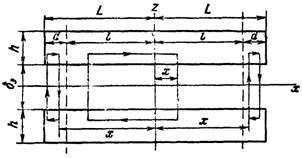
Рис. 2.12.
Рассматривается только поле индуктора при
токах в полосе, равных нулю (холостой ход или σ = 0). Активная
(обмотанная часть индуктора) имеет длину 2l.
Общая длина стальных участков индуктора 2L.
Волна линейной токовой нагрузки
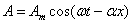
(2.37)
где
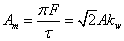
(2.38)
— амплитуда линейной нагрузки.
Считаем, что токи расположены в зазоре
равномерно по его высоте (см. 2.3). Зазор считается гладким, а насыщение зубцов
и стальных участков учитывается путем введения эквивалентного зазора δэ
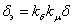
(2.39)
где
kδ — коэффициент воздушного зазора;
kμ — коэффициент насыщения стали зубцов
и др. участков.
Высота ярем индуктора равна
h. Индукция в зазоре имеет только
z–составляющую, постоянную по высоте зазора.
Введем обозначения:
B
— индукция в активной зоне
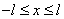 ; ;
Вл — индукция в зазоре
при
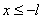 (левый
шунтирующий край); (левый
шунтирующий край);
Вп — индукция в зазоре
при
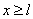 (правый
шунтирующий край); (правый
шунтирующий край);
Вя — индукция в ярме
активной зоны;
Вял — индукция в ярме
левого шунтирующего края;
Вяп — индукция в ярме
правого шунтирующего края;
Фlл
— поток в ярме в сечении при
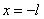
Фlп
— поток в ярме в сечении при
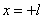
Составляющие положительны, если совпадают
по направлению с положительными направлениями координатных осей.
Покажем здесь общий план составления
исходного уравнения и нахождения его решения, опуская для краткости подробности,
которые читатель легко найдет, обращаясь к основной литературе.
На основе закона полного тока
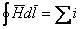 . .
Из рис. 2.12 для контуров имеем:
 (2.40)
(2.40)
Индукция в ярме
 (2.41)
(2.41)
После подстановки имеем:
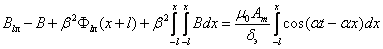 (2.42)
(2.42)
где
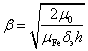 (2.43)
(2.43)
После дифференцирования дважды по х имеем
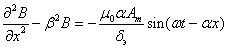 (2.44)
(2.44)
Решение этого уравнения имеет вид
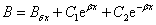 (2.45)
(2.45)
Здесь Вδх — частное решение уравнения
(2.44), которое можно представить в виде
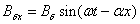 (2.46)
(2.46)
Нормальная составляющая индукции Вδ в
соответствии с общей теорией электрических машин
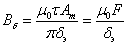 (2.47)
(2.47)
где
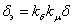 . .
Согласно (2.45)
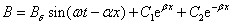 (2.48)
(2.48)
Здесь
Bδ — амплитуда индукции бегущего поля
при отсутствии краевых эффектов, второй и третий члены связаны с краевым
эффектом.
Так как в левом и правом шунтирующих
участках токи равны нулю, имеем:
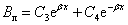 (2.49)
(2.49)
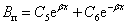 (2.50)
(2.50)
Опуская довольно сложный процесс
последовательного определения постоянных С1,
C2, С3, С4
окончательно имеем:
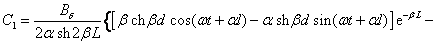
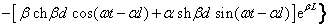 (2.51)
(2.51)
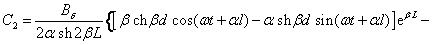
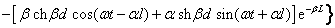 . .
Решения 2.51 записаны в общем виде. Для упрощения вида
решения примем
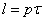 , где р —
целое число (четное число полюсов индуктора) , где р —
целое число (четное число полюсов индуктора)
Тогда:
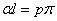
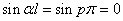
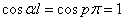
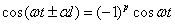
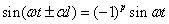
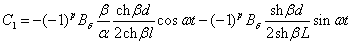 (2.52)
(2.52)
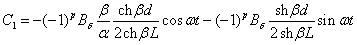 (2.53)
(2.53)
После подстановки в (2.48) окончательно имеем
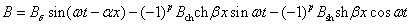 (2.54)
(2.54)
Здесь Bch
— амплитуда пульсирующего во времени поля, распределенного вдоль зазора по
закону гиперболического косинуса. Bsh
— амплитуда пульсирующего во времени поля, распределенного вдоль зазора по
закону гиперболического синуса.
Отношение:
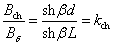 (2.55)
(2.55)
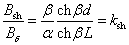 (2.56)
(2.56)
Если ярма не насыщены
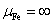 ,
то ,
то
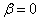 и и
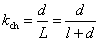 ; ;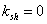 (2.57)
(2.57)
а (2.54) переходит к виду
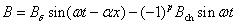 (2.58)
(2.58)
Из (2.58) следует, что при отсутствии
насыщения пульсирующее поле только одно, и оно тем меньше по сравнению с
бегущим, чем длиннее индуктор (d мало зависит
от l).
Характер распределения толя вдоль индуктора
лучше исследовать, получив огибающие поля.
Для этого возьмем
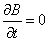 : :
Представив (2.54) в виде
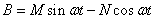
где
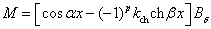
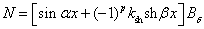
после
дифференцирования по t
имеем
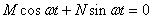
Отсюда
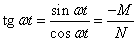
и
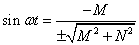 ; ;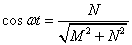
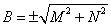
Окончательно имеем выражение:
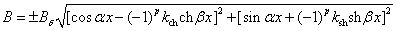 (2.58)
(2.58)
которое и дает уравнение огибающей
индукции.
Для
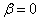 ; ;
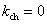
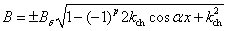 (2.59)
(2.59)
Вид огибающих индукция для индуктора с
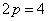 и и
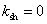 показан
на рис. 2.13. показан
на рис. 2.13.
Итак, магнитное поле вдоль зазора
неравномерно, что усложняет анализ ЛАД при движении вторичного тела. Однако этот
интересующий нас случай рассматривается в следующей главе.
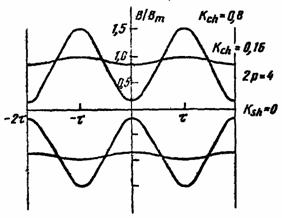
Рис. 2.13.
|
