2.3. Решение задачи с использованием модели,
представленной на рис. 2.3
При рассмотрении этой модели исходные
уравнения остаются прежними, однако, так как плотность тока распределена в
зазоре решения, получаются другими. Плотность возбуждающего тока можно записать
как
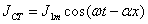 (2.22)
(2.22)
где
J1m—амплитуда
плотности тока, не зависящая от координат.
Комплексная амплитуда может быть записана в виде
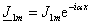 (2.23)
(2.23)
Считая, что суммарная линейная плотность
тока обеих обмоток определяется как и раньше по (2.19) и распределена по
координате z зазора равномерно, можно написать
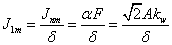 (2.24)
(2.24)
Индуктор
по-прежнему, неограниченный в направлении осей х, и у и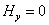 ; ;
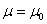 ; ;
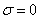 и
в исходных уравнениях имеются правые части: и
в исходных уравнениях имеются правые части:
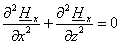 (2.25)
(2.25)
т.к. 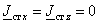 ; ;
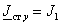 , ,
а 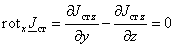
и 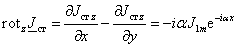 . .
Составляющие вектора
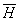 как
и раньше должны быть бегущими волнами: как
и раньше должны быть бегущими волнами:
Соответственно комплексные амплитуды будут
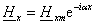 ; ;
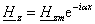 (2.27)
(2.27)
где
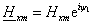 и
и 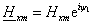 . .
После подстановки в (2.25) имеем:
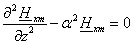 (2.28)
(2.28)
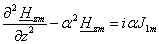 (2.29)
(2.29)
Решение (2.28) имеет вид
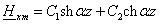 (2.30)
(2.30)
Так как токи на поверхностях стальных
индукторов отсутствуют а 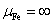 ,
при ,
при 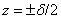 составляющие
Нхт на границах равны нулю составляющие
Нхт на границах равны нулю
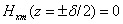 и
магнитные линии входят в индукторы перпендикулярно. и
магнитные линии входят в индукторы перпендикулярно.
Подстановка в (2.30) непосредственно дает
значение постоянных С1 и С2
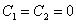 (2.31)
(2.31)
Это значит, что в
этой модели по высоте всего зазора 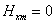 и
линии магнитного поля везде перпендикулярны поверхностям индукторов. и
линии магнитного поля везде перпендикулярны поверхностям индукторов.
Составляющая Нzт
определяется из уравнения
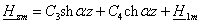 (2.32)
(2.32)
где H1m—частное
решение неоднородного уравнения с правой частью, a
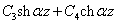 —
решение однофазного уравнения без правой части. —
решение однофазного уравнения без правой части.
H1m.
должно быть константой, так как J1m
— константа. Поэтому
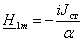 (2.33)
(2.33)
Из условия
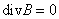
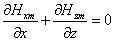 . .
Но
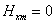 везде.
Значит, остается принять везде.
Значит, остается принять 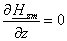 или или
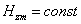 . .
Значит
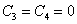 и
окончательно имеем и
окончательно имеем
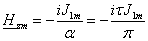 (2.34)
(2.34)
а также
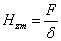 (2.35)
(2.35)
или
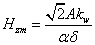 (2.36)
(2.36)
Таким образом здесь математически строго
доказана картина магнитного поля в зазоре, если тангенциальная составляющая
вектора Н принимается равной нулю, а токи распределены внутри зазора.
Характер поля в зазоре по ширине индуктора показан на рис.2.7.
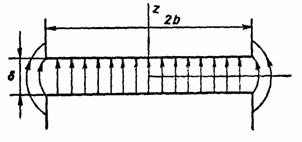
Рис. 2.7.
|
