2.1. Общие замечания о характере поля в
индукторе линейной асинхронной машины и постановка задачи
для его рассмотрения
В предыдущих разделах уже указывалось на
особенности магнитной цепи индуктора ЛАД и явления, связанные с его конечными
размерами. Эти явления называются краевыми эффектами. Разомкнутости
магнитопроводов ЛАД, обуславливают появление кроме бегущего поля неподвижных в
пространстве и пульсирующих во времени полей. Прежде чем перейти к рассмотрению
этой сложной задачи имеет смысл рассмотреть картину поля в зазоре идеального, т.
е. бесконечного плоского индуктора, в котором краевые эффекты отсутствуют. Это
позволит нам познакомиться с методологией расчета поля индуктора ЛАД и
особенностями выбора той или иной расчетной модели. На рис. 2.1 показана часть
бесконечно длинного индуктора, охватывающего два полюсных деления 2τ.
Наличие двусторонней зубчатости и дискретный характер расположения в пазах
проводников с токами осложняют задачу в такой степени, что ее решение становится
проблематичным. С целью упрощения исходной модели считают индукторы гладкими
(без пазов) и дискретные проводники с токами заменяют эквивалентными токовыми
слоями (настилами). Считают также, что магнитная проницаемость индукторов
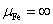 ,
а ,
а 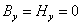 (в
направлении оси у индуктор также имеет бесконечные размеры). Схема такой
модели показана на рис. 2.2. Как видно из рисунка магнитное поле в зазоре
содержит две составляющих: нормальную Нz
и тангенциальную Нх (рассматривается первичное поле индуктора,
т. е. поле в режиме идеального холостого хода или при нулевой проводимости
вторичного элемента). (в
направлении оси у индуктор также имеет бесконечные размеры). Схема такой
модели показана на рис. 2.2. Как видно из рисунка магнитное поле в зазоре
содержит две составляющих: нормальную Нz
и тангенциальную Нх (рассматривается первичное поле индуктора,
т. е. поле в режиме идеального холостого хода или при нулевой проводимости
вторичного элемента).
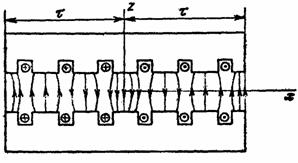
Рис. 2.1.
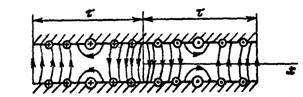
Рис. 2.2.
Обычно составляющая Нх
много меньше Нz, вместе с тем учет
обеих составляющих усложняет расчеты.
В теории электрических машин обычно
считают, что в зазоре существует только z —
составляющая возбуждающего (первичного) поля Hz,
а две другие составляющие
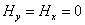 . .
Бегущая волна магнитного поля при этом
имеет вид
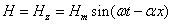 . .
|




 |
