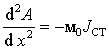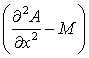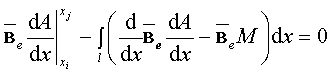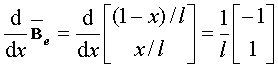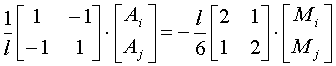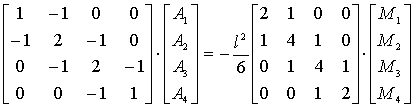1.4. Пример расчета поля с помощью МКЭ

Решить уравнение

 ,

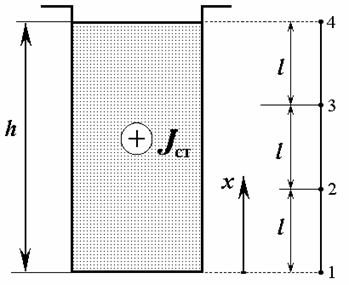
описывающее одномерное магнитное поле рассеяния в пазу с током электрической машины (рис. 1), методом конечных элементов, используя метод Галеркина. Высота проводника в пазу h = 0,03 м. Граничные условия: А_(х=0) = 0, dА/dх_(х=0) = 0. Плотность тока определяется условием  М = – m₀ J_СТ = 10. Сравнить полученные результаты с результатами расчета другими методами.

Решение.

1. Разобьем область поля на три элемента (рис. 1) одинаковой длины  l = 0,01 м. Так как задача одномерная, то каждый элемент представляет собой отрезок прямой с двумя узлами на концах. Будем считать (см. рис. 1), что знак “+” указывает на то, что ток в пазу направлен от нас за плоскость чертежа и имеет отрицательное значение, согласующееся с условием задачи.

2. Аппроксимируем, аналогично (1.32), векторный потенциал А(x) внутри элемента полиномом с двумя коэффициентами:

А(x) = a₁ + a₂ х .

Потенциалы узлов элемента

А(x_i)  = А_i ;   А(x_j) = А_j .

Система уравнений для узлов элемента согласно (1.35):

А_i = a₁ + a₂ х_i ,

А_j = a₁ + a₂ х_j .

3. В результате решения последней системы уравнений относительно a₁ и a₂  и подстановки в аппроксимирующий полином, получим уравнение для А(x, y) согласно (1.36), записанное через узловые значения  А_i  и А_j при расположении начала координат на дне паза

А(x) = [(х_j – х)/l ]× А_i + [(х – х_i)/l ] × А_j .

4. Запишем последнее уравнение относительно локальной системы координат  X  при расположении начала координат в i-м узле элемента, что упрощает последующие вычисления

А(x) = b_ei  × А_i + b_ej  × А_j ,

где     х = х_i + X ;      b_ei = (1– X /l );     b_ej = (X /l );

или в матричной форме

А(x) = [b_ei  b_ej] ×=×_{е ,}

где   = colon ( b_ei, b_ej );  _е = colon ( А_i, А_j ).

5. Сформируем систему алгебраических уравнений конечного элемента на основе метода Галеркина интегрированием уравнения вида (1.41)

^{×dх = 0 .}

Проинтегрируем записанное уравнение по частям. После интегрирования получим:

 ^,

где

 .

Уравнение для конечного элемента окончательно примет вид

  .

6. Запишем систему алгебраических уравнений для всей области, просуммировав матрицы в общих узлах элементов

  .

7. Решим полученную алгебраическую систему уравнений относительно узловых функций векторного магнитного потенциала.

Решение первого уравнения относительно А₂ с учетом заданного граничного условия  А₁ = 0  при  х = 0  имеет вид:

А₂ = (2М₁+М₂) .

Решение уравнений относительно А₃  и  А₄  подчиняется общему выражению

А_n+1 = 2 А_n – А_n–1 + (М₁ + 4М₂ + М₃) ,             где    n = 2, 3.

Учитывая, что  l = h/3 = 0,01,  М₁ = М₂ = М₃ = М₄ = М = 10,   окончательно имеем

А₁ = 0,     А₂ = 0,0005,     А₃ = 0,002,     А₄ = 0,0045.

8. Следует отметить, что точное решение исходного одномерного уравнения Пуассона при заданных граничных условиях путем его прямого интегрирования приводит к выражению

А(х) = – 0,5m₀ J_СТ × х ² ,

подстановка в которое узловых значений  х  дает результаты, точно совпадающие с полученными с помощью МКЭ.

9. Решим задачу с помощью МКР. Конечно-разностная форма одномерного уравнения Пуассона имеет вид

(А_n+1 – 2 А_n + А_n–1 ) / l ² = М  .

Тогда  рекуррентная  формула  для  определения  искомой  функции  в  n +1-м   узле по двум предыдущим будет

А_n+1 = 2 А_n ­– А_n–1 + l ² М  .

С помощью этой формулы при заданных на дне паза граничных условиях первого и второго рода можно определить векторный магнитный потенциал во втором узле путем введения в расчетную сетку дополнительного нулевого узла (позволяющего учесть граничные условия второго рода присваиванием нулевому узлу значения искомой функции первого узла). Конечно-разностная форма для граничного условия второго рода на дне паза записывается в следующем виде:

(А₁ ­– А₀ )/l = 0 ,

откуда имеем

А₀ = А₁ .

Однако в результате последовательного применения рекуррентной формулы получаем результаты, сильно отличающиеся от приведенных выше. Это связано с тем, что учтены не все условия на границе (при n = 1). Действительно, уравнение для узла  на границе, по которому определяется потенциал  А₂ ,  должно иметь коэффициент  0,5  перед плотностью тока, так как узел на границе только сверху граничит с током:

А₂ = 2 А₁ ­– А₀ + 0,5× l ² М  .

С учетом граничных условий выражение для определения потенциала А₂  имеет вид

А₂ = 0,5× l ² М  .

Потенциалы остальных узлов определяются по приведенной выше рекуррентной формуле.

Легко убедиться, что при подстановке числовых значений получим результаты, полностью совпадающие с рассчитанными с помощью МКЭ.

Обратим внимание на то, что в рассмотренном примере система алгебраических уравнений в МКР, так же, как и в МКЭ, решалась прямым методом на основе рекуррентных соотношений. Это оказалось возможным благодаря заданию на дне паза граничных условий первого и второго рода.