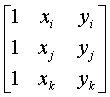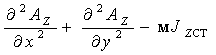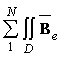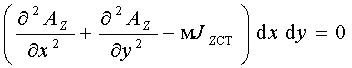1.3. Метод конечных элементов

Выше были сформулированы суть, основные достоинства и преимущества МКЭ в сравнении с МКР. Здесь мы более подробно опишем содержание МКЭ, рассмотрим особенности построения его алгоритма и простейший пример расчета поля.

Разбиение области на конечные элементы. В МКЭ расчетная область разбивается на элементы конечного размера в общем случае нерегулярной структуры. При расчете двумерных полей наибольшее распространение получили треугольные и прямоугольные элементы с прямолинейными сторонами. Размеры элементов и их ориентация выбираются исходя из условия конкретной задачи. Число узлов и их расположение в конечном элементе зависит от порядка интерполяционного полинома, описывающего распределение искомой функции внутри элемента. При использовании треугольного элемента с линейной интерполяцией элемент имеет три узла, так как полином содержит три коэффициента и требуется задание потенциалов в трех точках. Если используют квадратичную интерполяцию, то для определения шести коэффициентов полинома необходимо задать потенциалы шести узлов, принадлежащих элементу. В этом случае необходимо добавить еще три узла – по одному на каждую сторону элемента. Таким образом, вопрос о выборе вида конечного элемента решается с учетом порядка интерполяции и, как следствие, точности решения задачи.

Уравнение конечного элемента. Как уже было сказано, в пределах каждого элемента искомая функция, например, векторный магнитный потенциал, аппроксимируется полиномом n-й степени координат. Число коэффициентов аппроксимирующего полинома равно числу узлов используемого конечного элемента. Полиномы и расположение узлов элемента должны быть такими, чтобы сохранилась непрерывность искомой функции вдоль границ элемента. Для простоты рассмотрим двумерную задачу с линейной аппроксимацией искомой функции в каждом конечном элементе (в качестве примера выберем конечный элемент треугольной формы с прямолинейными сторонами):

А(x, y) = a₁ + a₂ x + a₃ y .                                      (1.32)

В матричной форме (1.32) принимает вид

А(x, y) = ^Т ×,                                                (1.33)

где  – вектор-столбец коэффициентов полинома конечного элемента

 = colon (a₁, a₂, a₃) ;

 – вектор-столбец координат

 = colon (1, x, y) ;

 Т – знак транспонирования.

В узлах треугольного конечного элемента, координаты которого (x_i , y_i), (x_j , y_j), (x_k , y_k), искомая функция принимает значения соответственно А_i , А_j , А_k . Записав (1.32) для трех узлов  конечного элемента, получим систему уравнений

А_i = a₁ + a₂ x_i + a₃ y_i ,

А_j = a₁ + a₂ x_j + a₃ y_j ,                                             (1.34)

А_k = a₁ + a₂ x_k + a₃ y_k ,

которую можно в матричной форме записать следующим образом:

_е = [Y] ,                                                       (1.35)

где _е – вектор-столбец векторных магнитных потенциалов в узлах элемента

_е = colon (А_i, А_j, А_k ) ;

[Y] – матрица координат узлов элемента

^{[Y] =  .}

Решив (1.35) относительно вектора коэффициентов  и подставив последний в полином (1.33), после преобразования получим

А(x, y) = ×_е ,                                                (1.36)

где  – вектор-столбец интерполяционных функций или функций формы конечного элемента, зависящих от координат узлов данного элемента

 = colon (b_ei, b_ej, b_ek ) = [Y]^–1Т  .                                (1.37)

Выражение (1.36) является уравнением конечного элемента.

Уравнения всей расчетной области. Интерполяционные функции  и узловые значения каждого элемента _е  представляют в общей для всей области расчета системе координат при общей нумерации узлов и элементов. Для этого проводят упорядоченную сквозную нумерацию всех узлов и элементов. Порядок нумерации узлов и элементов имеет большое значение при формировании и решении системы уравнений в МКЭ.

Матрица коэффициентов системы алгебраических уравнений является разреженной и ленточной. При этом ширина ленты зависит от способа нумерации узлов. Принципы, которые берутся в основу наилучшей с точки зрения наименьшей ширины ленты нумерации узлов, достаточно просты. Нумерацию следует производить так, чтобы разность номеров узлов, примыкающих к данному узлу, была наименьшей. Для этого при нумерации нужно обходить узлы в направлении наименьшего размера расчетной области, соблюдая неизменность направления, например, слева направо и снизу вверх.

Для всей расчетной области D уравнения можно записать путем суммирования по всем узлам области

А(x, y) = × ,                                                (1.38)

где  – вектор-столбец интерполяционных функций расчетной области D ;

  – вектор-столбец векторных магнитных потенциалов в узлах расчетной области D.

Элементы вектора , являющиеся интерполяционными функциями, изменят свои значения по отношению к элементам вектора , поскольку они зависят от числовых значений координат узлов расчетной области. При этом значение каждой из функций отлично от нуля только лишь внутри соответствующего ей элемента. Таким образом, каждое уравнение в (1.38) содержит неизвестное значение искомой функции в узлах и коэффициенты формы элементов.

С точки зрения выбора интерполяционных функций МКЭ занимает промежуточное место между МКР и методом Ритца [12, 13]. В МКЭ эти функции непрерывны не во всей расчетной области, а лишь в соответствующем им элементе. Вне этого элемента они имеют нулевые значения. В частном случае, когда элемент стянут в точку, приходим к МКР. Если же всю расчетную область рассматривать как один элемент, то получим метод Ритца.

Формирование системы алгебраических уравнений. Систему алгебраических уравнений для потенциалов всех узлов, т.е. узловых значений искомой функции , в МКЭ можно получить различными способами: методом Ритца, методом Галеркина [12, 13] и др. В первом случае уравнения потенциалов узлов отыскивают из условия минимума энергетического функционала, а во втором – из условия ортогональности невязки решаемого дифференциального уравнения и интерполяционных функций МКЭ.

Известно, что решением уравнения (1.26) для магнитного поля является такая функция А(x, y), которой соответствует наименьшее значение энергии магнитного поля. Поэтому искомый потенциал можно найти, обращая в минимум функционал I (А), соответствующий или пропорциональный энергии магнитного поля. В частности, для уравнения (1.26) с учетом однородных граничных условий (условий Неймана) энергетический функционал имеет вид:

I (А) =  1/2 [( dA/dx )²+ ( dA/dy )²] dx dy  –   2m  J_СТ А dx dy .     (1.39)

Алгебраическую систему уравнений для потенциалов узлов можно получить также, используя метод Галеркина, т.е. исходя из условия ортогональности невязки уравнения поля и базисных (интерполяционных) функций МКЭ. Так при решении уравнения (1.26), учитывая, что его невязка равна

I (А) =  ,                                 (1.40)

приближенное решение задачи можно записать в виде

 ,             (1.41)

где  N – число элементов области.

Метод Галеркина является наиболее эффективным методом, с помощью которого можно получить приближенное решение исходного дифференциального уравнения. Кроме того, применение вариационного подхода к решению уравнений с несимметричными операторами, например, при расчете квазистационарных полей, формально не обосновано так же строго, как использование метода невязок Галеркина. Учитывая, что метод невязок можно применить для получения уравнений не только при расчете стационарных и квазистационарных гармонических, но и переменных полей, целесообразно с единых позиций использовать этот путь получения алгебраических уравнений МКЭ [6].

В результате решения (1.41) с учетом суммирования по N элементам расчетной области получаем систему алгебраических уравнений вида

[K]×= ,                                                    (1.42)

где [K] – матрица коэффициентов, как уже было сказано, имеющая ленточную структуру; – вектор-столбец искомых потенциалов в узлах расчетной сетки; – вектор-столбец правых частей, не зависящий от искомых потенциалов и определяемый сторонними источниками тока и граничными условиями с известными значениями потенциалов.

При формировании матрицы [K] узлы с заданными значениями потенциалов (при наличии граничных условий Дирихле) рассматривают как обычные, а на завершающем этапе матрицу [K] "подправляют", перенося известные значения потенциалов в правую часть  уравнения (1.42).

С точки зрения времени и точности решения системы уравнений важными характеристиками матрицы  являются степень заполненности ее ненулевыми элементами, характер их расположения, а также число обусловленности c . Чем меньше ненулевых элементов в матрице и чем ближе они располагаются к диагонали, образуя узкую ленту, тем более эффективным оказывается численное решение системы уравнений. Число обусловленности влияет на трудоемкость решения, чем оно больше, тем выше трудоемкость.

Как правило, матрица [K] в МКЭ является слабозаполненной. Важной ее характеристикой является ширина ленты, которая зависит от порядка нумерации узлов. Чем меньше ширина ленты, тем экономичнее использование памяти ЭВМ и решение системы уравнений. Принципы, которые берутся в основу для получения наименьшей ширины ленты, кратко изложены выше. Однако, как правило, вычислительные программы осуществляют автоматически нумерацию узлов, не предусматривая интерактивного вмешательства. В противоположность этому, выбор числа узлов и характера сетки обычно доступны пользователю, что позволяет влиять на число обусловленности матрицы.

Оценить число обусловленности c достаточно сложно. При использовании нерегулярных сеток число c  зависит как от числа элементов N, так и от отношения наибольшего  h_max  и наименьшего  h_min  размеров сторон элементов [6]:

c º N× h_max / h_min .

Рост c до значений 10⁷–10⁸ приводит к потере точности в последних 7-8 разрядах результата. При больших значениях c ошибки вычислений могут привести к недостоверным результатам. На практике число c определяется как свойствами задачи (отношениями магнитных или диэлектрических проницаемостей), так, в частности, и формой и числом элементов. При формировании сетки из треугольных элементов, их следует выбирать так, чтобы они были близки к равносторонним, избегая применения вытянутых треугольников с малыми углами при вершинах (меньше 30^о).

При плохой обусловленности системы уравнений для повышения точности расчетов переходят к вычислениям с двойной точностью, приводящей, однако, к удвоению объема требуемой памяти ЭВМ. Другой способ заключается в использовании интерполяционных полиномов второго и более высоких порядков, позволяющий увеличить точность решения при тех же размерах элементов.

С учетом отмеченных выше замечаний система уравнений (1.42) решается с помощью любой стандартной процедуры, в результате чего находится распределение векторного потенциала  A  в узлах, а по (1.36), (1.38) и во всех элементах расчетной области D.