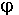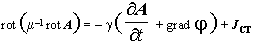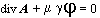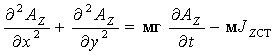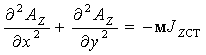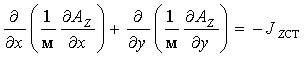|
|
|||||||||||||||||||
|
1.1. Уравнения электромагнитного поля
|
|||||||||||||||||||
|
Электромагнитное поле – это неразрывно связанные между собой и порождающие друг друга переменные электрическое и магнитное поля. Впервые понятие “электромагнитное поле” было введено и математически строго описано Джеймсом Клерком Максвеллом. Уравнения Максвелла были опубликованы им в 1873 году в книге “Трактат об электричестве и магнетизме”, т.е. почти 130 лет тому назад. Громоздкий механистический вывод отдельных уравнений был опубликован в его более ранних статьях. В “Трактате” же Максвелл их вывел с помощью аппарата векторного анализа, показав, что переменные электрическое и магнитное поля находятся в неразрывной взаимосвязи, совокупность которых представляет собой единое электромагнитное поле. Основными векторами, характеризующими электромагнитное поле, являются индукция B и напряженность H магнитного поля, смещение D и напряженность E электрического поля и плотность электрического тока J. В указанных современных обозначениях система уравнений Максвелла, заключающая в себе теорию электромагнитного поля, записывается следующим образом. Вектор магнитной напряженности H должен
удовлетворять первому уравнению Максвелла
утверждающему, что вихрь
магнитного поля создается полным током, определяемым плотностью тока
проводимости J и тока смещения
Второе уравнение Максвелла отражает закон электромагнитной индукции, открытый впервые в 1831 году Фарадеем rot E = – Это уравнение говорит, что любое изменение индукции магнитного поля приводит к возникновению вихревого электрического поля с электрической напряженностью E. Ленц в 1832 году вслед за открытием Фарадея показал, что под действием электрической напряженности E в замкнутом контуре возникает электрический ток, направленный так, что его магнитное поле противодействует изменению исходного (знак “минус” в правой части уравнения). Третье уравнение Максвелла – это уравнение непрерывности div B = 0 , (1.3) означающее, что нет истоков магнитного поля, нет магнитных зарядов, что линии магнитного поля являются замкнутыми. Это уравнение является математической формулировкой взглядов Фарадея, поддержанных Максвеллом и заключающихся в том, что линии магнитного поля всегда замкнуты или, по крайней мере, не имеют ни начала, ни конца. И, наконец, четвертое уравнение Максвелла div D = r (1.4) означает, что электрическое поле образуется зарядами, плотность которых равна r, и линии этого поля начинаются и кончаются на этих зарядах. Это уравнение часто называют дифференциальной формой электростатической теоремы Гаусса. Именно великий Гаусс в Германии довел до совершенства теорию потенциала, нашедшую широкое применение в электричестве и магнетизме. Основные четыре уравнения Максвелла следует дополнить соотношениями, связывающими между собой значения векторов электромагнитного поля B, H, D, E и J:
где m – магнитная проницаемость; e – диэлектрическая проницаемость; g – удельная электропроводность среды. В то время прямых доказательств теории Максвелла не было, поэтому слишком уж радикальными казались его выводы. А ведь два первых уравнения привели Максвелла к предсказанию существования электромагнитных волн и электромагнитной природы света. Он предсказал существование давления света и рассчитал его величину. Немецкий физик Генрих Герц, создавший вибратор электромагнитных волн и экспериментально доказавший их существование, так отзывался об уравнениях Максвелла: “Трудно избавиться от чувства, что эти математические формулы живут независимой жизнью и обладают своим собственным интеллектом, что они мудрее, чем их первооткрыватель, и что мы извлекаем из них больше, чем было заложено в них первоначально”. Сейчас, спустя более столетия, трудно даже себе представить, что в области электричества и магнетизма нет ни одного факта, не укладывающегося в рамки этой системы четырех максвелловских уравнений. В электромеханических устройствах частоты токов, создающих электромагнитное поле, обычно невысоки, а емкостные связи пренебрежимо малы по сравнению с индуктивными. Поэтому токи смещения в этих устройствах практически не проявляются. В соответствии с этим система уравнений электромагнитного поля упрощается и принимает вид rot H = J , (1.6) rot E = – div B = 0 , (1.8) где уравнения связи
Во многих случаях и вторым уравнением в указанной системе можно пренебречь и рассматривать стационарное магнитное поле, созданное системой постоянных токов. Такое же упрощение системы (1.6)–(1.8) справедливо и для полей переменных токов невысокой частоты, если в области существования этих полей нет массивных электропроводящих материалов и действием вихревых токов на результирующее поле можно пренебречь. В этом случае поле, созданное мгновенными значениями системы переменных токов также описывается уравнениями (1.6), (1.8). Решение системы уравнений Максвелла представляет
собой весьма сложную задачу. Поэтому для приведения этой системы уравнений к
виду, более удобному для решения были введены вспомогательные функции: векторного A
и скалярного
Векторный магнитный потенциал A определяется выражением rot A = B . (1.10) В интегральной форме выражение для векторного магнитного потенциала определяет его физический смысл: циркуляция векторного магнитного потенциала по замкнутому контуру равна магнитному потоку Ф, пронизывающему этот контур
В плоскопараллельном поле вектор A лежит в плоскости, перпендикулярной направлению вектора B. Для стационарного поля замкнутых токов вектор A удовлетворяет условию непрерывности div A = 0 . (1.12) Для описания магнитного поля в областях, не занятых токами, удобно использовать понятие скалярного магнитного потенциала, определяемого равенством H = – grad
В общем случае плотность токов проводимости состоит из плотности вихревых токов J В и плотности сторонних токов JСТ : J = J В + JСТ . (1.14) Переменный сторонний ток является источником переменного магнитного поля. Вихревые токи возникают в электропроводящих массивах под действием ЭДС, наведенной переменным магнитным полем. Не изменяя величины стороннего тока, вихревой ток приводит к его перераспределению в поперечном сечении массивного проводника. На основе уравнений Максвелла в средах с нелинейными магнитными характеристиками с помощью векторного магнитного потенциала можно записать уравнение, описывающее электромагнитное поле для произвольно изменяющихся во времени распределенных переменных токов, включая вихревые токи в массивах. Из (1.7) с учетом (1.10) имеем: rot (Е + Поскольку векторный магнитный потенциал определяется
согласно (1.10) с точностью до градиента произвольной скалярной функции, в том
числе и
rot grad а также (1.15), получаем: Е + Определив Е из (1.17) и подставив в выражение для J из (1.9), получим из (1.6), (1.7) с учетом (1.10) уравнение в векторной форме для неоднородного магнитного поля в нелинейной ферромагнитной среде
Решение (1.18) представляет значительные сложности. Задача существенно упрощается для линейной ферромагнитной среды, когда m = const. В этом случае магнитную проницаемость в (1.18) можно вынести за знак rot. Тогда с учетом соотношения векторного анализа rot rot А = grad div А – div grad А (1.19) и принятия условия калибровки
получим уравнение поля, которое называется уравнением диффузии div grad А
=
m
g или, что то же самое,
Ñ
2A =
m
g В декартовой системе координат для плоскопараллельного поля (1.22) принимает вид
Для случая синусоидально изменяющихся токов уравнение диффузии можно представить в комплексной форме, которое называется уравнением Гельмгольца
Ñ
2 Если в области существования поля отсутствует возможность возникновения вихревых токов (нет электропроводящих массивов) и токами смещения можно пренебречь и, тем более, если поле создается распределенными постоянными токами, то уравнение (1.22) преобразуется в уравнение Пуассона Ñ 2 A = – m J , (1.25) которое в двумерной декартовой системе координат принимает вид
Для случая нелинейной ферромагнитной среды двумерное стационарное магнитное поле описывается уравнением
В области существования поля, где токи отсутствуют, уравнение (1.25) принимает вид Ñ 2 A = 0 (1.28) и называется уравнением Лапласа. Уравнение Лапласа, записанное относительно скалярного магнитного потенциала, имеет вид, аналогичный (1.28) Ñ 2 j = 0 . (1.29) Решение задачи расчета поля в терминах скалярного магнитного потенциала (1.29) имеет заметные преимущества при ее решении с помощью МКР в случае, когда область поля содержит протяженные границы раздела сред сталь-воздух с бесконечной магнитной проницаемостью стали. В этом случае протяженность границ с детерминированным скалярным магнитным потенциалом (граничные условия первого рода или граничные условия Дирихле) будет преобладать над протяженностью границ, имеющих граничные условия второго рода или условия Неймана, когда искомая функция на границе задана выражением dj /d n = 0 (здесь n – направление нормали к границе). Таким образом, на большей части границ значения j будут известны, что значительно ускоряет итерационный процесс решения задачи расчета поля с помощью МКР. Следует отметить, что решение задачи с протяженными границами второго рода с помощью МКЭ не приводит к каким-либо осложнениям. Решением уравнений (1.21)–(1.28) и (1.29) является распределение в области расчета соответственно векторного или скалярного магнитных потенциалов. Зная их распределение, можно найти, например для плоскопараллельной задачи, между заданными точками а и b соответственно поток на единицу длины вглубь расчетной области как разность векторных магнитных потенциалов в этих точках Фab = Aa – Ab (1.30) или падение магнитного напряжения между этими точками как разность скалярных магнитных потенциалов Uab =
ja – jb = На практике для расчета поля к его уравнениям необходимо добавить уравнения, описывающие границы всех областей расчета с различными физическими характеристиками, а также граничные условия для векторов магнитного поля на их внешних границах. Основные положения теории электромагнитного поля и методы их расчета приведены, например в [1–3]. |
||||||||||||||||||
|
вверх страницы |
|||||||||||||||||||

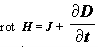
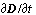 . Введение
тока смещения в правую часть уравнения в дополнение к току проводимости было
гениальным открытием Максвелла. Ток смещения, введенный Максвеллом, возникает
под действием изменяющегося во времени
. Введение
тока смещения в правую часть уравнения в дополнение к току проводимости было
гениальным открытием Максвелла. Ток смещения, введенный Максвеллом, возникает
под действием изменяющегося во времени 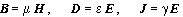 ,
, .
.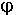
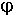
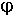 , то, учитывая, что
, то, учитывая, что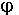 = 0
,
= 0
,