|
Рассмотрим последнее уравнение
совместно с каждым из приводимых далее уравнений (определяющих
один из участков граничной линии
 )
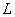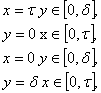(38)
Нетрудно убедиться, что искомая
линия поля прямую, задаваемую уравнением
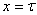 не
пересекает. Действительно, из (37) следует
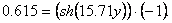
Это уравнение относительно
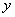 не
имеет корней на отрезке
 .
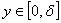Несовместными оказывается и пара уравнений, включающая в себя
уравнение линии поля и уравнение
 .
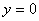В то же время подстановка в уравнение линии поля (35)
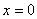 позволяет
определить 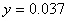 м,
при котором искомая линия поля пересекает участок границы,
задаваемый уравнением
.
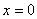Таким образом, в рассматриваемом примере точка
 .
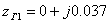Вторая точка искомой линии,
принадлежащая граничной линии
 ,
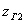определится после подстановки
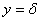 в
уравнение линии поля и последующего решения уравнений
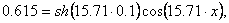(39)
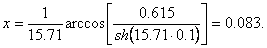(40)
|
