|
К п. 1—21. Построение линий
поля. К линиям поля
относятся:
а) линии потока;
б) эквипотенциальные линии.
Определение.
Линией потока называется такая линия, на которой значение
функции потока неизменно. Уравнение линии потока
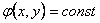 .
Эквипотенциальная линия поля — это такая линия, на которой
значение скалярного магнитного потенциала неизменно. Ее
уравнение имеет вид .
Эквипотенциальная линия поля — это такая линия, на которой
значение скалярного магнитного потенциала неизменно. Ее
уравнение имеет вид
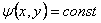 . .
Если по условию задачи требуется
провести через заданную точку
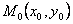 линии
поля обоих видов, то необходимо выполнить следующие операции: линии
поля обоих видов, то необходимо выполнить следующие операции:
а) в выражения для
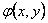 и и
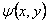 ,
заданные по условию задачи или определенные тем или иным
способом к моменту построения линий поля, подставляем координаты
точки ,
заданные по условию задачи или определенные тем или иным
способом к моменту построения линий поля, подставляем координаты
точки 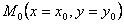 и
определяем значения функции скалярного потенциала и
определяем значения функции скалярного потенциала
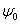 и
функции потока и
функции потока 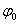 в
этой точке: в
этой точке:
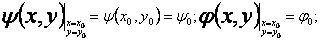
б) записываем уравнения искомых
линий поля (в неявном виде)
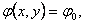 (31) (31)
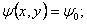 (32) (32)
в) рассматриваем совместно
уравнения линий поля, полученные в предыдущем пункте, совместно
с уравнением граничной линии
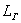 области
и определяем в результате решения системы двух уравнений точки
пересечения искомой линии поля с границей области. Найденные
граничные точки искомых линий поля определяют диапазон изменения
переменных области
и определяем в результате решения системы двух уравнений точки
пересечения искомой линии поля с границей области. Найденные
граничные точки искомых линий поля определяют диапазон изменения
переменных 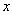 (или (или
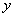 ),
при последующем поиске из уравнения линии поля (см. п. б)
соответствующих значений ),
при последующем поиске из уравнения линии поля (см. п. б)
соответствующих значений
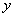 (или (или
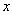 ).
При отыскании граничных точек линий поля полезно иметь в виду,
что линии поля обязательно пересекают возбужденный участок
границы области; ).
При отыскании граничных точек линий поля полезно иметь в виду,
что линии поля обязательно пересекают возбужденный участок
границы области; |