|
Преобразование функции
комплексного потенциала
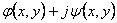 в
функцию одного комплексного переменного в
функцию одного комплексного переменного
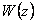 .
В соответствии с определением комплексной потенциальной функции
и полученными выражениями для .
В соответствии с определением комплексной потенциальной функции
и полученными выражениями для
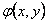 (27) (27)
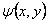 (28),
имеем (28),
имеем
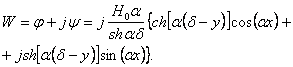 (29) (29)
Введем временно переменные
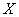 и и
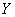 взамен взамен
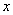 и и
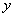 в
соответствии с уравнениями в
соответствии с уравнениями
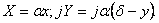
Обращаясь к (63)—(67), замечаем,
что содержимое в скобках правой части (29) может быть
представлено в следующем виде:
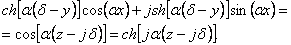
Учитывая последнее соотношение,
искомое выражение для функции
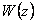 ,
можно записать в следующей форме: ,
можно записать в следующей форме:
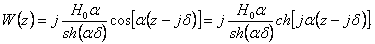
Правильность полученного выражения можно
проверить, рассчитав с его помощью комплекса напряженности
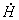 магнитного
поля магнитного
поля
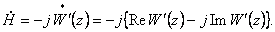 (30) (30)
Убедитесь в том, что после
несложных преобразований и выделения действительной и мнимых
частей (функциональных, зависящих от переменных
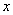 , ,
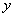 )
получаются выражения для составляющих напряженности )
получаются выражения для составляющих напряженности
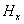 и и
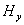 ,
полностью совпадающие с искомыми выражениями для ,
полностью совпадающие с искомыми выражениями для
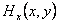 , ,
 . .
|