|
Откуда,
учитывая 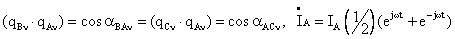 , получим , получим
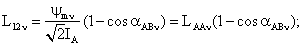 (105) (105)
б) путем суммирования
потокосцеплений самоиндукции данной фазы и взаимоиндукции других
фаз с данной из уравнения
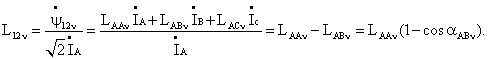 (106) (106)
Полные индуктивные сопротивления
фазы для произвольной гармонической (при
n =
l получим главное индуктивное
сопротивление фазы) могут быть определены по формулам
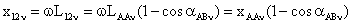 (107) (107)
где для
определения сопротивления
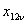 следует воспользоваться указаниями к пп. 6,7. следует воспользоваться указаниями к пп. 6,7.
Токи обратной последовательности
образуют на временной диаграмме симметричную систему комплексов
так же, как и токи прямой последовательности. Поэтому расчет
индуктивных сопротивлений самоиндукции и взаимоиндукции ничем не
отличается от вышеизложенного. При определении индуктивных
параметров для токов нулевой последовательности необходимо
учесть, что эти токи во всех трех фазах в каждый момент времени
равны по величине и одинаковы по направлению. Поэтому
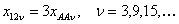 (108) (108)
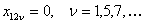 (108) (108)
|