|
Аналогично можно определить и
проводимость зазора на одно зубцовое деление для четного поля
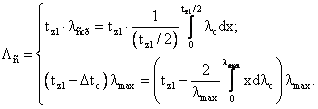 (85) (85)
Проще однако найти вначале разность
проводимостей 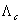 и и
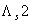 , которая, как показывает анализ, равна
постоянному числу, не зависит от относительных параметров , которая, как показывает анализ, равна
постоянному числу, не зависит от относительных параметров
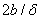 , ,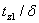 . Действительно, воспользовавшись
соотношениями (70) и (79) и обозначив искомую разность . Действительно, воспользовавшись
соотношениями (70) и (79) и обозначив искомую разность
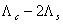 через 2Q,
получим рис.2.7 через 2Q,
получим рис.2.7
|
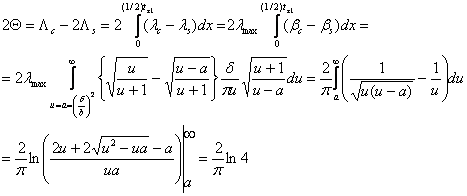 |
(86) |
откуда,
учитывая (82)-(84)
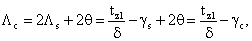 (87)
(87)
то есть
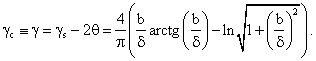 (88) (88)
При выполнении заданий п.п. 1-4
следует отчетливо представлять себе, что скалярные магнитные
потенциалы обоих сердечников одинаковы и равны, например, нулю
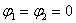 . Последнее равенство можно считать следствием
того, что ни многофазная обмотка в целом, ни ее «элементарная»
составляющая – зубцовый контур –не создают при своем возбуждении
униполярного магнитного потока через зазор. Следует правильно
интерпретировать часто употребляемое выражение «распределение
скалярного магнитного потенциала
Y(х,
t) (МДС F(x,
t)) на поверхности возбужденного
сердечника...». В действительности же следует говорить о
распределении скалярного магнитного потенциала на обращенной к
зазору стороне условно непроницаемой поверхности,
непосредственно примыкающей к граничной поверхности сердечников
(см. рис. 2.7). . Последнее равенство можно считать следствием
того, что ни многофазная обмотка в целом, ни ее «элементарная»
составляющая – зубцовый контур –не создают при своем возбуждении
униполярного магнитного потока через зазор. Следует правильно
интерпретировать часто употребляемое выражение «распределение
скалярного магнитного потенциала
Y(х,
t) (МДС F(x,
t)) на поверхности возбужденного
сердечника...». В действительности же следует говорить о
распределении скалярного магнитного потенциала на обращенной к
зазору стороне условно непроницаемой поверхности,
непосредственно примыкающей к граничной поверхности сердечников
(см. рис. 2.7).
|





 |