|
Таким образом, основная задача
построения МДС F(x,
t) сводится к тому, чтобы по
заданным токам ветвей
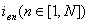 ) и известной структуре обмотки (т. е. по
заданным числам пазов на полюс и фазу q,
полюсов 2р, витков в отдельной катушке
wk,
шагах обмотки и пр.) определить токи зубцовых контуров ) и известной структуре обмотки (т. е. по
заданным числам пазов на полюс и фазу q,
полюсов 2р, витков в отдельной катушке
wk,
шагах обмотки и пр.) определить токи зубцовых контуров
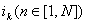 . Сводя неизвестные токи зубцовых контуров в
столбцовую матрицу . Сводя неизвестные токи зубцовых контуров в
столбцовую матрицу 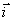 , содержащую z1
строк, и токи ветвей в столбцовую матрицу , содержащую z1
строк, и токи ветвей в столбцовую матрицу
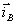 , содержащую N строк, выразим искомые
токи зубцовых контуров через заданные токи ветвей и неизвестную
пока матрицу преобразований [F],
содержащую столько же строк, сколько имеется неизвестных токов
зубцовых контуров, т. е. z1, и
число столбцов, совпадающее с числом ветвей
N: , содержащую N строк, выразим искомые
токи зубцовых контуров через заданные токи ветвей и неизвестную
пока матрицу преобразований [F],
содержащую столько же строк, сколько имеется неизвестных токов
зубцовых контуров, т. е. z1, и
число столбцов, совпадающее с числом ветвей
N:
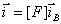 (10)
(10)
С целью выяснения структуры матрицы
преобразования [F] составим
вначале z1 уравнений,
связывающих между собой искомые токи зубцовых контуров
независимым образом. Условимся считать ток паза
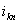 положительным, если этот ток имеет
направление «от нас», и отрицательным, если этот ток направлен
«на нас». При выборе знака тока для токов зубцовых контуров
будем руководствоваться следующим правилом: ток зубцового
контура положительным, если этот ток имеет
направление «от нас», и отрицательным, если этот ток направлен
«на нас». При выборе знака тока для токов зубцовых контуров
будем руководствоваться следующим правилом: ток зубцового
контура 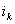 считается положительным, если создаваемый им
магнитный поток совпадает с направлением от сердечника в сторону
зазора. считается положительным, если создаваемый им
магнитный поток совпадает с направлением от сердечника в сторону
зазора.
Возвращаясь к искомой системе из
z1 уравнений для токов зубцовых
контуров, замечаем, что z1-1
уравнений можно написать, используя очевидные соотношения,
связывающие ток произвольного«k»-го
паза ink с токами смежных с
этим пазом токов зубцовых контуров (рис.2.1).
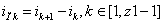 ,
(11) ,
(11)
которые целесообразнее представить в виде
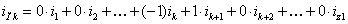
|





 |