|
С учетом
коэффициента скоса расчетное выражение для обмоточного
коэффициента приобретает следующий вид:
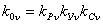 (61)
(61)
Расчетные выражения для скорости
перемещения в пространстве для «ν» -й гармонической МДС в
электрических рад/с (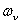 ) и в геометрических рад/с ( ) и в геометрических рад/с (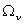 ) определятся исходя из неизменности фазы
рассматриваемой волны МДС в данной точке с угловой координатой ) определятся исходя из неизменности фазы
рассматриваемой волны МДС в данной точке с угловой координатой
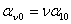 в момент времени t
и в точке с угловой координатой в момент времени t
и в точке с угловой координатой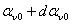 , куда переместится волна МДС за малый
промежуток времени dt , куда переместится волна МДС за малый
промежуток времени dt
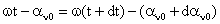 , (62) , (62)
откуда
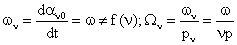 . (63) . (63)
При определении функциональной
зависимости для индукции магнитного поля В(х, у,
t), в том числе и на поверхности
z1 = 0 невозбужденного
сердечника В(х, t,
y = 0),
ее удобно представить в виде произведения двух функций В'(у)
и В"(х, t), последняя из
которых очевидно повторяет закономерность изменения от тех же
переменных результирующей МДС
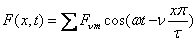 , возбуждающей магнитное поле в зазоре. Для
практических целей вполне достаточным оказывается знание
распределения индукции магнитного поля на поверхности
невозбужденного сердечника (y
= 0) , возбуждающей магнитное поле в зазоре. Для
практических целей вполне достаточным оказывается знание
распределения индукции магнитного поля на поверхности
невозбужденного сердечника (y
= 0)
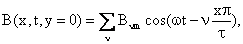 (64) (64)
где
амплитуду индукции для «μ»-ой гармонической
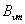 можно определить исходя из точного решения
задачи (см. далее) из уравнения (y
= 0, t
= 0) можно определить исходя из точного решения
задачи (см. далее) из уравнения (y
= 0, t
= 0)
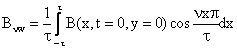 (65) (65)
или на
основе условно определяемого понятия удельной магнитной
проводимости зазора для «ν»-й
гармонической индукции
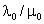 из уравнения из уравнения
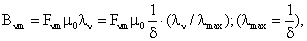 (66) (66)
|