3.3. Продольный краевой эффект при движении вторичного тела и его влияние на
основные характеристики ЛАД
Общие замечания. Конечная длина индукторов ЛАД
обуславливают появление в возбуждающем поле кроме бегущей волны две стоячие
пульсирующие волны. При наличии в зазоре вторичного проводящего и движущегося
тела в последнем возникает не только ответные бегущие волны тока и поля, но и
дополнительные токи и поля, оказывающие, как правило, тормозное действие,
увеличивающие потери и снижающие к. п. д. машины в целом. Вредное влияние
продольного краевого эффекта может быть очень значительным и его изучение для
некоторых типов ЛАД должно представлять центральную задачу. В последующих
разделах этой главы будет показано, что все типы ЛАД условно могут быть
разделены на 3 группы, в которых проявление краевого аффекта имеет различный
характер и в зависимости от этого должно учитываться обязательно или может не
учитываться вовсе.
Проблеме изучения продольного краевого эффекта посвящено
большое количество работ. Обычно на современном этапе делаются попытки решения
двух и трехмерных задач, что неизбежно приводит к численному анализу и
чрезвычайно затрудняет понимание физики явления и его особенностей. Поэтому
представляется целесообразным рассматривать одномерную модель с такими
упрощениями, которые минимально искажают реальную физическую картину явления и в
то же время позволяют максимально упростить математическое решение задачи. С
этой целью мы воспользуемся расчетной моделью, предложенной я проанализированной
А. И. Вольдеком.
Основные допущения и решение задачи
Расчетная модель представлена на рис. 3.3.
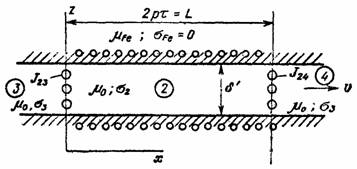
Рис. 3.3.
Основные допущения следующие:
1.
Магнитопроводы индукторов имеют
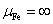 , ,
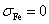 и
бесконечны в направлениях (+, –) оси х. и
бесконечны в направлениях (+, –) оси х.
2.
Поперечный краевой эффект отсутствует, т. е. ширина индукторов по оси
у неограничена.
3.
Индукторы гладкие (не имеют тазов). Их влияние учитывается введением
эквивалентного зазора 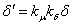 . .
4.
Немагнитный зазор 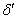 полностью
занят проводящим вторичным телом (без зазора). полностью
занят проводящим вторичным телом (без зазора).
5.
Обмотка индуктора имеет четное число полюсов и создает синусоидальную
бегущую волну поля, возбуждающие токи (токи индукторов) расположены в зазоре
(см. 2.3) и их распределение от координаты z не
зависит.
6.
Компенсирующие элементы (к. э.) и их токи распределены в виде слоев
поверхностных токов на границах активной зоны с линейными плотностями
J23 и J24.
Это допущение подчинено допущению 5, где принята идеальная бегущая волна поля.
Решение проводится в неподвижной системе координат жестко
связанной с индуктором ЛАД.
При этих допущениях задача является одномерной и векторы
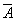 , ,
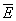 и и
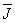 имеют
только одну составляющую, направленную по оси у, а вектор имеют
только одну составляющую, направленную по оси у, а вектор
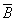 —
только по оси z. —
только по оси z.
Плотность тока индукторов при такой формулировке задачи
записывается аналогично (2.22); (2,23) и (2.24).
Суммарные комплексные амплитуды линейной плотности тока к.
э. на границах активной зоны (2) запишутся, как
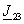 и и
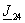 . .
Решение резонно провести для векторного потенциала от
первичных и вторичных токов.
Из условия задачи
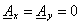 ; ;
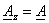 . .
Исходное уравнение для А в зоне 2 на основе (l.25)
приобретает вид:
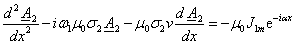 (3.12) (3.12)
В зонах 3 и 4 сторонний (возбуждающий) ток равен нулю:
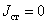 .
Поэтому в зонах 3 и 4 имеем: .
Поэтому в зонах 3 и 4 имеем:
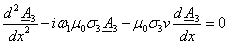 (3.13) (3.13)
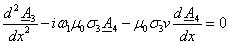 (3.14) (3.14)
Решение уравнения (3.12) состоит из частного решения и
общего решения однородного уравнения без правой части. Частное решение
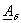 соответствует
идеальному бегущему магнитному полю, и должно иметь такую же зависимость от
координаты х, как и плотность тока соответствует
идеальному бегущему магнитному полю, и должно иметь такую же зависимость от
координаты х, как и плотность тока
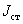 . .
Поэтому
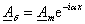 (3.15) (3.15)
После подстановки (3.15) в (3.12) простых преобразований
имеем
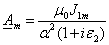 (3.16) (3.16)
где
магнитное число Рейнольдса
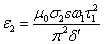 (3.17)
(3.17)
Общее решение однородного уравнения (3.12) теперь будет
иметь вид:
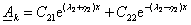 (3.18) (3.18)
где C21
я С22 — постоянные интегрирования;
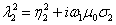 (3.19) (3.19)
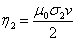 (3.20)
(3.20)
Полное решение уравнения для векторного потенциала
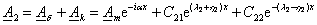 (3.21) (3.21)
В зонах 3 и 4 при
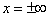 векторный
потенциал должен обращаться в нуль. Поэтому для зоны 3 решение возможно только в
виде векторный
потенциал должен обращаться в нуль. Поэтому для зоны 3 решение возможно только в
виде
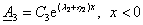 (3.22)
(3.22)
Здесь также С3—постоянная
интегрирования
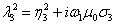 (3.23) (3.23)
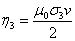 (3.24)
(3.24)
Для зоны 4 аналогично:
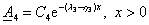 (3.25) (3.25)
а
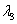 и и
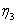 те
же, что в (3.23) и (3.24). те
же, что в (3.23) и (3.24).
Для подробного анализа решения нам потребуется определение
всех постоянных интегрирования.
Так как 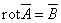 ,
а ,
а 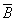 имеет
только одну составляющую Bz и вектор имеет
только одну составляющую Bz и вектор
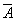 только
y‑составляющую только
y‑составляющую
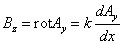 или или
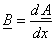 . .
На границах зоны 2 с зонами 3 и 4
имеем:
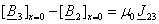 (3.26) (3.26)
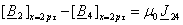 (3.27) (3.27)
Далее на основании (3.21), (3.22), (3.25), (3.26), (3.27)
получаем:
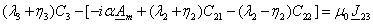 (3.28)
(3.28)
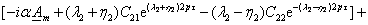
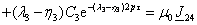
При получении (3.28) учтено, что
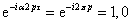 ,
т. к. р — целое число. ,
т. к. р — целое число.
На границах зон 2,3 и 2,4 должны быть непрерывны
касательные составляющие напряженности электрического поля
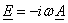
или
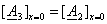 ; ;
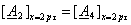 (3.29) (3.29)
Поэтому из (3.21), (3.22) и (3.24) имеем:
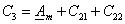 (3.30) (3.30)
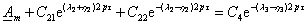 (3.30) (3.30)
Полученные уравнения позволяют получить выражения для всех
постоянных интегрирования:
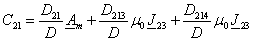 (3.31) (3.31)
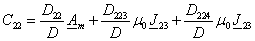
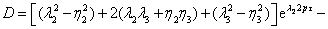
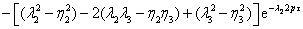 (3.32)
(3.32)
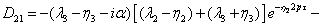
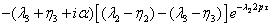 (3.33)
(3.33)
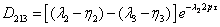 (3.34)
(3.34)
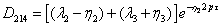 (3.35)
(3.35)
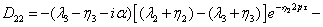
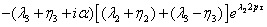 (3.36)
(3.36)
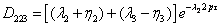 (3.37)
(3.37)
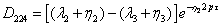 (3.38) (3.38)
Такие же выражения можно получить и для С3,
С4. Но при известных C21
и С22 это проще сделать непосредственно из (3.30).
|
