3.2. Поперечный краевой эффект. Принципы его определения
Примем расчетную модель как на рис. 3.1.
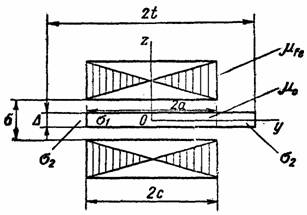
Рис. 3.1.
Магнитная проницаемость
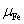 индукторов
равна бесконечности, а проводимость индукторов
равна бесконечности, а проводимость 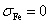 ;
токи индукторов распределены в зазоре между сердечниками равномерно по высоте и
образуют бегущую волну МДС. Электрическая проводимость полосы ;
токи индукторов распределены в зазоре между сердечниками равномерно по высоте и
образуют бегущую волну МДС. Электрическая проводимость полосы
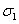 и и
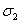 в
разных зонах, а магнитная проницаемость в
разных зонах, а магнитная проницаемость
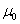 .
Скорость движения проводящего тела .
Скорость движения проводящего тела 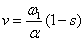 ,
где ,
где 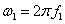 , ,
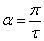 ; ;
s — скольжение, равное,
как обычно, 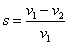 . .
Рассмотрим общий подход к решению задачи и проанализируем
основные результаты ее решения.
Результирующие значения индукции и напряженности магнитного
поля можно представить в виде двух слагаемых:
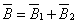 ; ;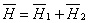
где
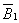 и и
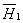 —
создаются токами индуктора; —
создаются токами индуктора; 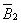 и и
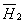 —
токами, индуктированными в проводящей полосе полем индуктора. —
токами, индуктированными в проводящей полосе полем индуктора.
В соответствии с 2.3 поле индуктора имеет только
z-составляющие. Очевидно, что индуктированные во
вторичном теле токи, тоже не зависят от z и
распределены по высоте зазора равномерно. Значит вторичное магнитное поле также
имеет только z-составляющие
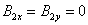 ; ;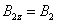
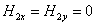 ; ;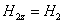
Однако вектор плотности тока во вторичном теле будет иметь
составляющие по осям у и х (рис. В.6). Векторный потенциал
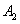 также
будет иметь составляющие по осям у и х. также
будет иметь составляющие по осям у и х.
Поскольку вектор Н имеет только одну составляющую
удобнее искать решение для Н, после определения которого можно с помощью
известных соотношений получить все остальные интересующие нас величины.
Общий вид исходного уравнения
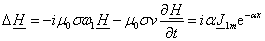 (3.1) (3.1)
Решая уравнения для зоны 1 и 2 и используя граничные
условия непрерывности для тангенциальных составляющих напряженности поля, и
нормальных составляющих плотности тока и вводя эквивалентную проводимость
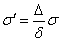 после
ряда преобразований получаем для интересующих нас величин выражения: для
активной зоны 1 после
ряда преобразований получаем для интересующих нас величин выражения: для
активной зоны 1
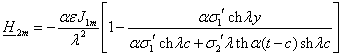 (3.2) (3.2)
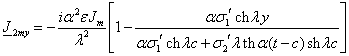 (3.3) (3.3)
Здесь
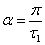
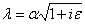 (3.4)
(3.4)
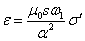
Величина ε, как уже указывалось выше, называется
магнитным числом Рейнольдса. По определению магнитное число Рейнольдса имеет
вид, аналогичный просто числу Рейнольдса
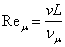 (3.5)
(3.5)
где v
— скорость, L — характерный линейный размер,
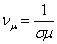 —
магнитная вязкость. —
магнитная вязкость.
Нетрудно убедиться, в том, что при выборе в качестве
характерного размера полюсного деления
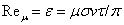
Из анализа выражений (3.2) и (3.3) следует, что
распределение поля и плотности тока неравномерно по координате у, что
ослабляет эффективность ЛАД. В этом смысле говорят об ослабляющем действии
поперечного краевого эффекта. Картина результирующего магнитного поля по ширине
индуктора показана на рис. 3.2.
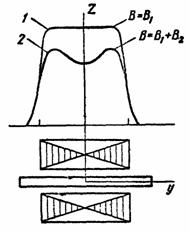
Рис. 3.2.
Кривая 1 соответствует
холостому ходу, кривая 2 — при наличии вторичного тела в зазоре. Из
рисунка видно, что вторичное поле не только искажает распределение по координате
у, но и уменьшает результирующее поле (оказывает размагничивающее
действие). Конечно, во всех рассматриваемых задачах первичное поле
B1 задано токами индуктора, которые
считаются (амплитуды) постоянными, т. е. и В1 —
постоянно.
При питании индуктора от источника напряжения картина будет
несколько иной, так как должно соблюдаться при этом постоянство потока.
Если подсчитать среднюю объемную удельную силу, возникающую
во вторичном теле
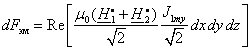
здесь Re
— вещественная часть комплексного числа, полное усилие, развиваемое ЛАД, будет
иметь вид:
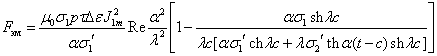 (3.6) (3.6)
В бесконечно широком индукторе
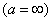 и и
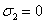 , ,
 : :
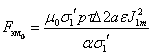 (3.7) (3.7)
Т.е. это есть сила, развиваемая ЛАД
при отсутствии поперечного краевого эффекта.
Выражение
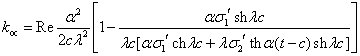 (3.8) (3.8)
может быть названо коэффициентом
ослабления эффективности ЛАД из-за действия поперечного краевого эффекта и
индуктивностью вторичного тела.
Согласно (3.6), (3.7) и (3.8) результирующее выражение для
силы равно
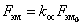 (3.9) (3.9)
Анализ выражения для koc
показывает, что наличие вылетов (t – с)
улучшает эффективность ЛАД. Аналогичное действие оказывает увеличение
электропроводности σ2 или наличия короткозамыкающих шин, аналогичные
короткозамыкающим кольцам обычного асинхронного двигателя. Однако при
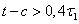 дальнейшее
увеличение эффективности практически прекращается. дальнейшее
увеличение эффективности практически прекращается.
В практических расчетах предпочитают увеличивать влияние
поперечного краевого эффекта более простыми формулами, уменьшающими
электрическую проводимость вторичного элемента. Например, многие используют
формулу, предложенную В. Е. Скобелевым
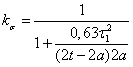 (3.10) (3.10)
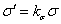 (3.11) (3.11)
B дальнейшем изложении будем считать, что поперечный эффект
определен и может быть рассчитай по тем или иным формулам. Это позволит
упростить расчетную модель для анализа действия продольного краевого эффекта.
Опять может быть использована одномерная модель ЛАД как
наиболее .простая и наглядная. Как и раньше мы не будем приводить на этих
страницах подробный ход решения уравнений и определения постоянных
интегрирования. Интересующийся читатель найдет эти подробности в
основополагающей литературе, список которой здесь приводится. В соответствии с
замыслом этого пособия наша цель выяснить достаточно строго основные проявления
главных особенностей ЛАД и провести конкретный их анализ. Расчет ЛАД, выбор
основных размеров ЛАД представляет, конечно, самостоятельную задачу, которая не
может быть затронута на этих страницах.
|
