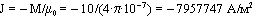2.10 Пример расчета

Решим двумерную задачу определения поля рассеяния в пазу с током, изображенном на рис. 1 в примере расчета гл. 1 с указанными в этом примере исходными данными. Так как задача двумерная, добавим к этим данным ширину паза b = 6 мм. Плотность тока в проводнике в соответствии с исходными данными параграфа 1.4:

Решение.
1. Для создания новой задачи выберем позицию New в меню Files и в появившемся окне введем имя файла задачи.

2. Выберем Миллиметры в позиции Length Units меню Options.

3. В диалоговом окне Описание задачи позиции Problem меню Edit выберем тип задачи – Магнитостатика, класс задачи – плоская и расчет Обычный.

4. Перейдем к редактированию модели: позиция Geometry меню Edit. Выберем позицию Keyboard меню Zoom редактора модели и введем значения размеров прямоугольника расчетной области: –15; 15; 0; 30.

5. Построим вершины расчетной области, выбрав позицию Add Vertex меню Model. Нажав клавишу Tab, введем координаты первой вершины: –3;0, фиксируя ввод клавишей Enter. Таким же образом вводим координаты остальных вершин: (3;0), (–3;30), (3;30).

6. Выбрав Add Edge и указав в окне ввода угол 0о для прямой линии, последовательно соединяем отрезками прямых все четыре вершины. Образовалась область расчета поля в виде одного прямоугольного блока.

7. В пункте меню Label присвоим блоку метку Ток, верхней стороне блока – метку D, а всем остальным сторонам – метку N.

8. Перейдем к построению сетки, выбрав в главном меню редактора позицию Mesh. Затем выберем позицию Set Spacing и в нижних вершинах зададим шаги дискретизации сетки, равными 2, а в верхних – равными 0,5. Перейдем к позиции Build Mesh и построим сетку.

9. Выходим из редактора модели и выбираем позицию Data пункта Главного Меню Edit для задания свойств материалов, источников и граничных условий. Для этого выберем Метки блоков и отредактируем метку Ток. В диалоговом окне этой метки введем относительную магнитную проницаемость меди, равную 1, рассчитанную выше плотность тока: –7957747 и нажмем кнопку Готово. Далее перейдем к Меткам сторон и зададим для метки D нулевые граничные условия Дирихле, а для метки N – условия Неймана. Выйдем из файла описания свойств, сохранив введенные данные.

10. Теперь можем перейти к позиции Главного Меню Results и решить задачу.

11. После решения задачи открывается окно постпроцессора с картиной поля в построенной области расчета, представляющей собой прямые линии, параллельные дну паза. Выберем позицию Edit Contour пункта меню постпроцессора X-Y Plot, далее в пункте Add Edge выделим одну из вертикальных стенок паза и сделаем два щелчка правой кнопкой мыши. После этого появится по умолчанию график распределения индукции вдоль этой стенки. Нажмем еще раз правую кнопку мыши, выберем в появившемся меню позицию View и в раскрывшемся окне выделим кнопку альтернатив под названием Потенциал. 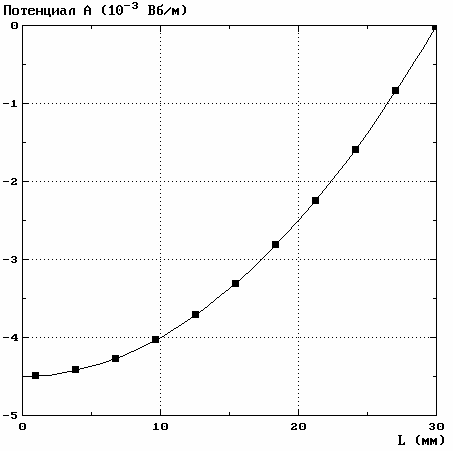Затем нажмем кнопку Готово.
После этого в большом окне постпроцессора появится график распределения векторного магнитного потенциала по высоте стержня, представленный на рис. 2.

Если иметь ввиду, что векторный магнитный потенциал определен с точностью до постоянной, а в данной задаче нулевое значение векторного магнитного потенциала было принято на верхней границе паза, то, мысленно переместив нулевое значение потенциала на дно паза, ось абсцисс на графике рис. 2 переместится вниз на – 4,5×10–3 Вб/м.

Тогда на этом графике значения векторного магнитного потенциала в узловых точках, соответствующих задаче параграфа 1.4, будут полностью совпадать с результатами, полученными ранее.

Рис. 2. Распределение векторного магнитного потенциала по высоте стержня

Кроме того, как видно из графика рис. 2, нарастание векторного магнитного потенциала в нижних слоях паза весьма слабое, что позволило в несколько раз увеличить шаг сетки у дна паза, а значит уменьшить и общее число узлов сетки до 278 против 1097, не понизив при этом точность решения поставленной задачи.

Обратим внимание на то, что одномерная постановка задачи в параграфе 1.4 вполне оправдана. Однако эта задача становится двумерной, если ввести толщину изоляции между проводником и границами паза. В этом легко убедиться, решив усложненную таким образом задачу и построив картину поля.