|
31. Магнитное поле возбуждается
постоянной разностью потенциалов
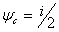 .
Известными считаются также комплексная потенциальная функция,
описывающая магнитное поле - в плоскости преобразования, а также
функция преобразования .
Известными считаются также комплексная потенциальная функция,
описывающая магнитное поле - в плоскости преобразования, а также
функция преобразования
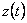 ,
связывающая верхнюю полуплоскость formula с областью
четырехугольника ,
связывающая верхнюю полуплоскость formula с областью
четырехугольника 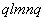 в
плоскости в
плоскости 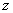 . .
Рассчитать и изобразить
графически распределение напряженности магнитного поля вдоль
границы области.
В соответствии с имеющейся на
кафедре электрических машин программой рассчитать, используя
программируемый микрокалькулятор типа МК-54 или МК-85, и.
построить затем на миллиметровке в удобном для обозрения
масштабе совокупность линий потока.
32. Магнитное поле в зазоре
возбуждается током, размещенным на дне бесконечно глубокого паза
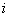 .
Известными предполагаются также комплексная потенциальная
функция .
Известными предполагаются также комплексная потенциальная
функция 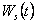 ,
описывающая нечетное поле в плоскости преобразования ,
описывающая нечетное поле в плоскости преобразования
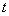 ,
и функция преобразования ,
и функция преобразования
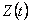 . .
Рассчитать и изобразить
графически распределение напряженности магнитного поля вдоль
границы области.
В соответствии с имеющейся на
кафедре электрических машин программой рассчитать, используя
программируемый микрокалькулятор типа МК-54 или МК-85, и
построить затем на миллиметровке в удобном для обозрения
масштабе совокупность линий потока.
33. Магнитное поле возбуждается
током зубцового контура. Представляя искомое магнитное поле
возбужденного зубцового контура в виде суммы составляющих его
четного и нечетного магнитных полей (см. задачи № 31 и 32
соответственно). Определить:
а) комплексную потенциальную
функцию, описывающую магнитное поле зубцового контура на
протяжении половины зубцового деления;
б) общее расчетное выражение для
напряженности магнитного
поля;
в) изобразить графически
распределение напряженности магнитного поля вдоль гладкой
поверхности невозбужденного сердечника. |