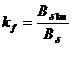Содержание

Часть 1

1.1

1.2

1.3

1.4

Часть 2

2.1

2.2

2.3

2.4

Часть 3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Литература

 Кафедра ЭМ

Применение полевых методов в электромагнитных расчетах

электрических машин

1.3.1. Коэффициенты формы поля возбуждения, потока возбуждения и расчетный коэффициент полюсного перекрытия явнополюсных синхронных машин

Для ненасыщенных машин эти коэффициенты вычисляются непосредственно по определяющим их выражениям:

                                                     (1.13)

                                                    (1.14)

                                                     (1.15)

Значение величин, входящих в (1.13) – (1.15), поясняются рисунком 1.12.

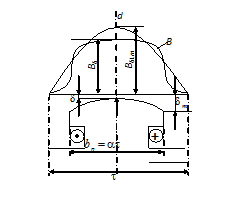
Рис. 1.12. К определению основных величин поля возбуждения

B_δ1m- амплитуда основной гармоники индукции поля в зазоре,

Ф_f1m- значение потока основной гармоники поля в зазоре

Ф_fm- наибольшее значение потока возбуждения на полюсном делении,

B_δ – значение индукции на оси полюса,
        B_δср – среднее значение индукции в зазоре

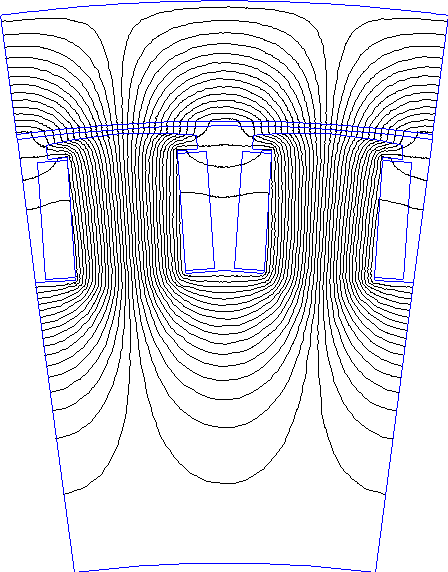
Рис. 1.13. Картина поля при холостом ходе

На рисунке 1.13, приведена картина поля в активной зоне явнополюсной синхронной машины при холостом ходе. На модели не воспроизводится зубцовая зона статора, однако кривые намагничивания стали статора и ротора заданы реальными. Основные размеры поперечного сечения машины (зазор, полюсное деление, диаметр расточки, размеры полюсов) взяты из примера расчета явнополюсного синхронного генератора в [1-5]. Плотность тока в обмотке возбуждения подобрана таким образом, чтобы индукции в ярмах и в воздушном зазоре были близки к реальным значениям. На рисунке виден след цилиндрической поверхности, проведенной в воздушном зазоре на середине его высоты. Распределение индукции, «измеренное» на этой поверхности и сохраненное в виде текстового файла, может быть подвергнуто гармоническому анализу. Кроме того, интегрирование нормальной составляющей индукции вдоль этого контура позволяет определить значение потока на полюсном делении и среднее значение индукции. Таким образом, на модели могут быть найдены все величины, необходимые для расчета коэффициентов ,  и  .

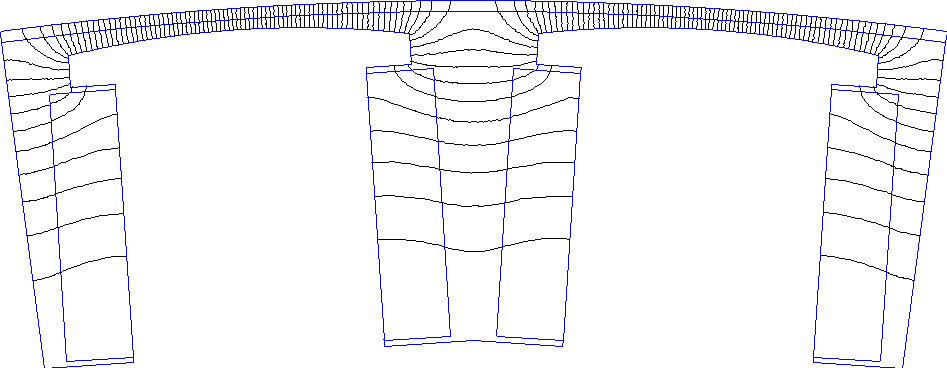
При задании постоянной и достаточно большой магнитной проницаемости для стали сердечников (µ_r = 10000) результаты получаются практически такими же, как и при моделировании нелинейных сталей (см. табл. 1.5).

На рис. 1.14 показана модель, в которой сталь статора и ротора не воспроизводится. Задание условий Неймана на поверхностях сердечников статора и ротора соответствует заданию бесконечной магнитной проницаемости стали.

Рис. 1.14. Картина поля при холостом ходе при задании условий Неймана на поверхностях сердечников статора и ротора.

На моделях, показанных на рисунках 1.13 и 1.14, воспроизведены полные периоды поля – по два полюсных деления. На боковых границах моделей при этом в общем случае должны быть заданы периодические граничные условия (при моделировании холостого хода в силу симметрии на этих границах могут быть заданы условия Неймана). Область задачи, однако, можно сократить, ограничившись моделированием одного полюсного деления и задав на боковых границах антипериодические граничные условия. «Измеренные» данные в этом случае перед тем, как подвергнуть гармоническому анализу, следует преобразовать так, чтобы они представляли весь период поля.

Таблица 1.5

1 – модель с воспроизведением нелинейных свойств сердечников

2 – модель с µ_r = 10⁴

3 – модель с граничными условиями Неймана (см. рис. 1.14)

4 – определение коэффициентов по [ГГ и СК].

При расчете коэффициентов , в ряде пособий по учебному проектированию (например, в [1-5]) рекомендуется учитывать насыщение зубцовой зоны с помощью коэффициентов насыщения k_za и k_zam .

                                                      (1.16)

                                             (1.17)

                                                   (1.18)

где F₁ – сумма падений магнитных напряжений в зубцовых зонах и ярмах статора и ротора, F_δ – магнитное напряжение воздушного зазора, δ_м, k_δ, и k_δм – максимальный зазор (под краем полюса) и коэффициенты зазора под серединой полюса (минимального) и максимального.

Для того чтобы учесть насыщение магнитопровода при определении коэффициентов  и  на конечно-элементных моделях, следует воспроизвести зубцовую зону, задав при этом нелинейные свойства стали статора и ротора. На рис. 1.15, показана модель гидрогенератора, имеющего основные размеры те же, что и генератор, взятый в качестве примера расчета в [1-5]. Размеры пазов и зубцов, однако, скорректированы таким образом, чтобы на полюсное деление приходилось целое число пазов.

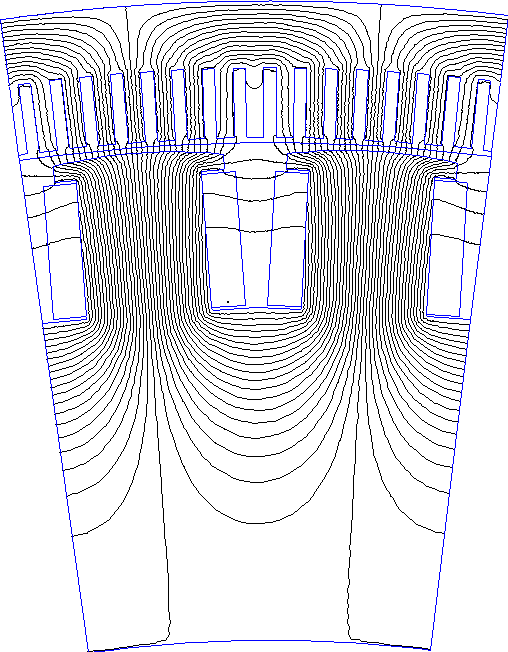
Рис. 1.15. Картина поля при холостом ходе при воспроизведении на модели зубцовой зоны статора и нелинейных свойств стали.

В табл. 1.6, приведены определенные по результатам моделирования значения коэффициентов и . В серии численных экспериментов варьировалась плотность тока на участках модели, соответствующих обмотке возбуждения от 0,5 до 2,2 А/мм², что соответствует изменению индукции в зубцах до 1,94 Т и в ярме статора до 1,51 Т. Индукция в сердечниках полюсов при этом изменялась до 2,02 Т, зубцовая зона демпферной обмотки не воспроизводилась.

Таблица 1.6  

  Назад   Продолжение