|
Уравнение для 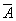
Часто вводится понятие векторного потенциала магнитного
поля А, который удовлетворяет условию
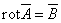 (1.16)
(1.16)
Векторный
потенциал 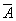 полностью
характеризует электромагнитное поле с точностью до некоторой постоянной, которая
может быть приравнена нулю. Определив полностью
характеризует электромагнитное поле с точностью до некоторой постоянной, которая
может быть приравнена нулю. Определив
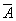 можно
последовательно определить все остальные неизвестные векторы поля можно
последовательно определить все остальные неизвестные векторы поля
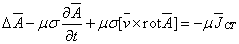 (1.17)
(1.17)
 Правые
части приведенных уравнений всегда известны или равны нулю, если сторонние токи
отсутствуют, а левые части содержат только одно неизвестное. Если среда
неподвижна — Правые
части приведенных уравнений всегда известны или равны нулю, если сторонние токи
отсутствуют, а левые части содержат только одно неизвестное. Если среда
неподвижна — 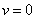 ,
то получаются автоматически уравнения для неподвижной среды (третьи члены
уравнений обращаются в нуль). Кроме того, если поле стационарно и не зависит от
времени, получаются уравнения Пуассона типа ,
то получаются автоматически уравнения для неподвижной среды (третьи члены
уравнений обращаются в нуль). Кроме того, если поле стационарно и не зависит от
времени, получаются уравнения Пуассона типа
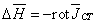
определяющие
стационарные электромагнитные поля в неподвижной среде.
Все рассмотренные уравнения являются
векторными и в декартовой системе координат (а также в других системах координат)
распадаются на три отдельных скалярных уравнения для каждой из координат в
отдельности. Каждое из скалярных уравнений решается общими методами,
применяющимися при решении дифференциальных уравнений в частных производных.
Однако для движущихся сред решения всегда сложны и всегда важно найти такие
упрощения или допущения при назначении граничных условий, которые не очень
сильно искажают картину реального поля и в то же время значительно облегчают
решение задачи в целом.
При анализе ЛАД часто считают, что все
величины изменяются по гармоническому закону во времени заведомо идеализируя
реальную картину. Однако эта идеализация позволяет упростить уравнения и их
решения путем введения комплексных амплитуд векторов поля.
Делается это так. Пусть вектор
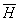 изменяется
по закону изменяется
по закону
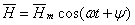 (1.18)
(1.18)
где Нт—максимальное (амплитудное) значение вектора в данной
точке пространства, ω —угловая частота, t —
время, ψ — начальная фаза.
Следует заметить, что Нт
является только функцией координат и не зависит от времени.
Из
известного соотношения
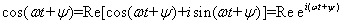
где i — мнимая единица, a Re
обозначает реальную часть комплексного числа, можно написать вместо (1.18)
выражение
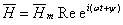 (1.19)
(1.19)
Если обозначить
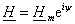 (1.20)
(1.20)
Это выражение можно назвать комплексной
амплитудой вектора 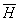 .
Вектор .
Вектор 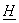 имеет
более сложный характер, чем вектор имеет
более сложный характер, чем вектор
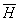 ,
так как его составляющие по координатным осям являются не скалярами, а
комплексными числами. ,
так как его составляющие по координатным осям являются не скалярами, а
комплексными числами.
Теперь вектор
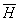 может
быть определен так может
быть определен так
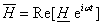 (1.21)
(1.21)
По аналогии вектор плотности стороннего тока можно записать
в виде
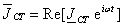 (1.22)
(1.22)
где
Jст — комплексная амплитуда сторонней
плотности тока.
Представив в аналогичной форме другие
векторы поля, подставив их в соответствующие уравнения и вынося после
дифференцирования общий множитель 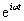 ,
и отбросив знак Re и сократив обе части уравнений на ,
и отбросив знак Re и сократив обе части уравнений на
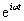 ,
получим в окончательной форме дифференциальные уравнения для комплексных
амплитуд: ,
получим в окончательной форме дифференциальные уравнения для комплексных
амплитуд:
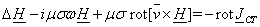 (1.23)
(1.23)
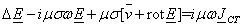 (1.24)
(1.24)
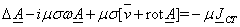 (1.25)
(1.25)
Каждое из этих уравнений раскладывается на
три по координатным осям. Переход к реальным векторам Н, E,
J осуществляется в обратном порядке, т. е.
найденную величину комплексной амплитуды, например
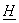 ,
умножают на ,
умножают на 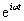 и
берут реальную часть полученного произведения. и
берут реальную часть полученного произведения.
Однако такой обратный переход часто просто
не нужен, так как при определении сил, мощностей потерь и т. д. достаточно
оперировать только комплексными амплитудами как это делается в теории переменных
токов.
Действительно, на переменном токе
осуществляют переход к комплексам аналогично:
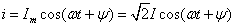
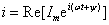
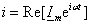
где
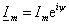 —
комплексная амплитуда тока. —
комплексная амплитуда тока.
Вводимые в теории переменных токов действующие значения
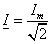 ; ;
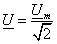
не вносят ничего нового и не
изменяют существо способа. В дальнейших главах всегда будет считаться, что все
величины изменяются синусоидально, а уравнения использоваться в комплексной
форме записи.
Для упрощения решений сложных дифференциальных уравнений
для Н, Е, А и т. д. вектор скорости
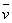 совмещают
с какой-либо координатной осью и считают ее постоянной. Например, если вектор совмещают
с какой-либо координатной осью и считают ее постоянной. Например, если вектор
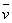 направлен
по оси х, то составляющие скорости направлен
по оси х, то составляющие скорости
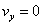 ; ;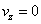 и и 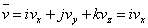 , ,
где i,
j, k, —
орты правовинтовой декартовой системы.
Используя основные соотношения векторного анализа, сложное
выражение типа 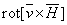 упрощается
и принимает вид: упрощается
и принимает вид:
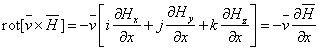 (1.26)
(1.26)
Очевидно, что уравнение (1.13) принимает вид:
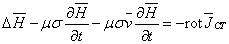 (1.27)
(1.27)
комплексное уравнение (1.23)
переходит в
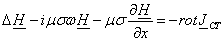 (1.28)
(1.28)
Учитывая, что вектор
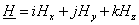 составляющие
уравнения (1.27) по координатным осям (скалярные уравнения) записываются в виде: составляющие
уравнения (1.27) по координатным осям (скалярные уравнения) записываются в виде:
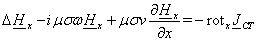
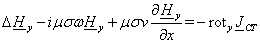 (1.29)
(1.29)
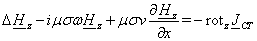
Аналогичным образом могут быть получены уравнения для Е
и А и их составляющих по координатным осям. Из-за ограниченности объема
данного пособия здесь они не приводятся и будут использованы при рассмотрении
конкретных задач. По этой же причине и из-за более сложного вида уравнения для
Н, Е и А в цилиндрических или другого вида криволинейных
координатах здесь тоже не рассматриваются. Все рассматриваемые задачи будут
только плоскими и используется прямоугольная система координат.
|
