1.1. Бегущее магнитное поле
Бегущее магнитное поле можно определить как
квазистационарное магнитное поле, синусоидально меняющееся во времени в каждой
точке пространства, причем все точки, имеющие одинаковую амплитуду и фазу
колебания во времени, перемещаются в пространстве прямолинейно с постоянной
скоростью v. Строго говоря, такое поле не
должно иметь ни начала, ни конца, т. е. оно должно простираться из бесконечности
в бесконечность.
На практике из-за ограниченной длины
индукторов такое идеальное поле реализовано быть не может. Однако, если общая
длина индуктора намного превышает длину полуволны (полупериода) поля, то
приближенно толе индуктора может определяться как бегущее. Особо следует
отметить, что скорость движения бегущего магнитного поля не имеет ничего общего
со скоростью распространения энергии, то есть скоростью распространения в
пространстве электромагнитной волны.
Скорость бегущего магнитного поля является
фазовой скоростью и зависит только от частоты тока, возбуждающего это поле, и от
геометрического распределения его в пространстве
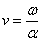
,где
ω — круговая частота возбуждающего тока;
 —
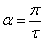параметр, определяемый длиной пространственной полуволны τ (полюсным
делением).
Эта скорость не связана с переносом энергии
и может быть поэтому как сколь угодно малой, так и бесконечно большой (например,
больше скорости света).
Бегущая волна может быть записана в виде
выражения
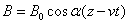(1.1)
где В —
вектор магнитной индукции; z — координата в
направлении движения волны; t—текущее время.
Пользуясь символическим методом изображения
гармонически меняющихся величин, это же выражение в комплексной форме имеет вид
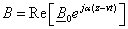(1.2)
В реальных индукторах ЛАД для уменьшения
состава высших пространственных гармонических поля обмотки выполняются обычно с
60° фазной зоной при 3-х фазном токе. Условно схема 3-х фазного индуктора
показана на рис. 1.1. Конечно, возможно выполнить индуктор и с 120° фазной
зоной, но такое включение применяется крайне редко.
В реальных индукторах из-за дискретного
расположения проводников в пазах, из-за наличия зубцов, ограниченности длины и
ширины форма бегущего магнитного поля не совпадает с формой чистой бегущей
волны, что сильно осложняет расчет ЛАД и решения полевых задач. Поэтому часто
вводятся упрощения (допущения) и условно считается, что индуктор ЛАД создает
идеальное бегущее поле. Такие индукторы обычно называют идеальными индукторами.
В идеальном индукторе распределение тока (плотности тока) вдоль направления
движения поля имеет форму идеальной бегущей волны. Ток протекает в бесконечно
тонком слое (токовом настиле) и имеет только одну составляющую, перпендикулярную
направлению движения поля, размеры индуктора в продольном и поперечном
направлениях считаются бесконечными.
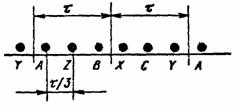
Рис. 1.1.
Математически такое распределение тока
может быть; записано при помощи функции.
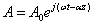(1.3)
Идеальный индуктор представляет собой
неограниченную плоскость, то поверхности которой в направлении координаты у
протекает ток (1.3).
Магнитная проницаемость индуктора при этом
часто принимается равной бесконечности, а характеристики рабочей среды
(вторичного элемента) могут быть любые.
|
