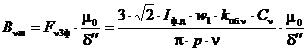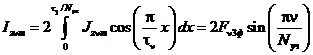Содержание

Часть 1

1.1

1.2

1.3

1.4

Часть 2

2.1

2.2

2.3

2.4

Часть 3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Литература

 Кафедра ЭМ

Применение полевых методов в электромагнитных расчетах электрических машин

2.4. Определение потерь в массивных сердечниках электрических машин

с помощью простых конечно-элементных моделей

 ( 1   2   3   4   5 )

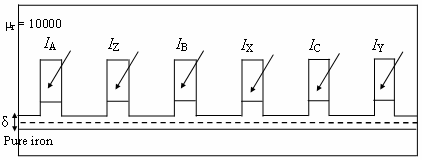
Рис. 2.41. Исходная модель №1 машины с массивным вторым сердечником

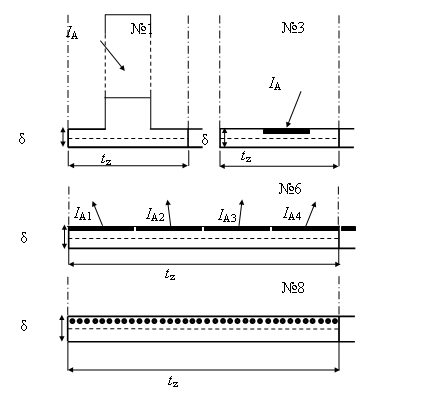
Рис. 2.42. Фрагменты моделей №№ 1, 3, 6 и 8 (по одному зубцовому делению)
 

Bначале сравнение моделей производилось по результатам решения магнитостатических задач. Плотности тока (и точечные токи) задавались равными мгновенным значениям соответствующих переменных (синусоидальных) величин в момент времени, когда ток в фазе А достигает максимума. Относительная магнитная проницаемость обоих сердечников принималась равной 10⁴ (либо, если не моделировался материал сердечника, на его границе задавалось условие Неймана). После расчета поля определялось распределение индукции вдоль поверхности, проходящей посередине воздушного зазора (след этой поверхности виден на рисунках 2.41 и 2.42), выполнялся гармонический анализ этого распределения и результаты моделирования сравнивались с расчетом по известным аналитическим выражениям.

Таблица 2.12

Амплитуды гармоник распределения индукции вдоль средней линии воздушного зазора, рассчитанные по аналитическим выражениям и определенные на различных моделях.

Как видно из таблицы, вынесение токов из пазов на уровень поверхности расточки при сохранении общей конфигурации активной зоны (модель №2) практически не отражается на гармоническом составе поля в зазоре. Однако модель №2 не проще и не быстрее модели №1 и ее следует рассматривать как промежуточный этап при переходе от модели с пазами к беспазовой модели. В модели №3, при гладких сердечниках, амплитуды гармоник заметно изменяются по сравнению с исходной моделью. Заметим, что увеличение зазора в k_δ раз (k_δ – коэффициент зазора), «восстанавливает» только 1-ю гармонику.

Среди моделей, в которых МДС обмотки статора представлены токовыми слоями на поверхности гладкого сердечника, наиболее точной является модель №8. Точечные токи, задаваемые на малых участках этой модели (N_уч = 360), вычисляются по известным аналитическим выражениям с учетом коэффициента влияния пазов C_ν:

амплитуда ν-й гармоники индукции, созданной МДС 3-фазной обмотки:

                                (2.4)

где    I_ф.д – действующее значение фазного тока, w₁ – число последовательных витков фазы, k_об.ν – обмоточный коэффициент, p – число пар полюсов,  -зазор, приведенный с учетом зубчатости второго сердечника.

Амплитуда линейной плотности поверхностного токового слоя:

,                                                                            (2.5)

где - амплитуда соответствующей гармоники распределения скалярного магнитного потенциала, .

Наибольшее значение «точечного» тока, соответствующего ν-й гармонике, задаваемое на элементарном участке токового слоя (зависит от числа участков N._уч):

                                           (2.6)

Фазовые углы распределений плотности тока и точечных токов в токовых слоях определяются конфигурацией модели и заданной на ней схемой обмотки. Так, общим началом отсчета всех гармоник МДС на модели №1 является точка на оси первого паза (с током I_A), а ось третьего зубца (между пазами с токами I_Z и I_B ) является магнитной осью всех гармоник.

Задавать значения точечных токов на большом числе элементарных участков лучше программным способом (в описании FEMM есть инструкции по программированию на языке Lua).

При моделировании переменного поля задание постоянной магнитной проницаемости на всем участке модели, соответствующем массиву, может привести к большой ошибке. Так, если для модели №1 задать µ_к = 10³ и σ₂ =10 МСм/м, потери во втором сердечнике составят ок. 10,5 Вт/мм (на 1 мм аксиальной длины модели), в то время как для массива с нелинейными свойствами (Pure iron, σ =10 МСм/м) потери при той же частоте существенно меньше – ок. 6 Вт/мм. В связи с этим сравнение моделей следует производить при задании для массива реальной кривой намагничивания.

  Назад   Продолжение