Расчет полей-2.4

Применение полевых методов в электромагнитных расчетах электрических машин

2.4. Определение потерь в массивных сердечниках электрических машин

с помощью простых конечно-элементных моделей

( 1 2 3 4 5 )

Из сравнения рисунков 2.36 и 2.38 видно, что гармонический состав поля на поверхности массивного сердечника практически повторяет гармонический состав кривой МДС верхнего сердечника.

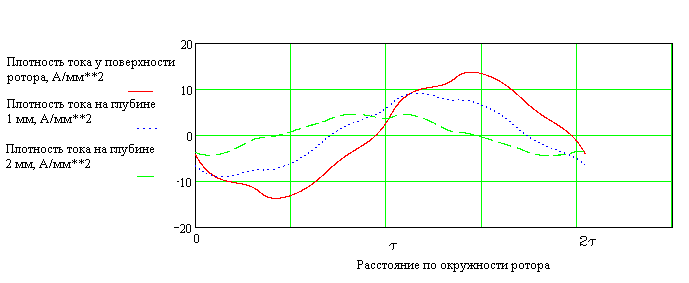
Рис. 2.39. Распределение плотности тока на различной глубине массивного сердечника. Изменяется не только амплитуда, но и фазовый угол распределений плотности тока.

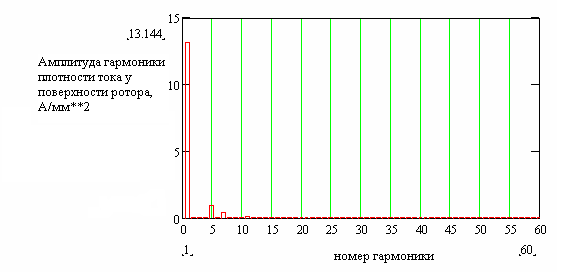
Рис. 2.40. Гармонический состав распределения плотности тока вблизи поверхности нижнего сердечника.

Несмотря на то, что высшие гармоники индукции на поверхности нижнего сердечника довольно значительны, в распределении плотности индуктированного тока они выражены гораздо слабее (см. рис. 2.40).

Число узлов в модели – 37339, время решения 5 минут. Потери в массивном сердечнике составили: в первом, ближайшем к воздушному зазору слое – 2,1185 Вт/мм (на один мм аксиальной длины модели), во втором слое – 0,7617 Вт/мм, в третьем слое – 0,1338 Вт/мм. Общие потери оказались равными 3,0141 Вт/мм.

Для оценки точности решения и оценки влияния дробности сетки конечных элементов на результат расчета численный эксперимент был повторен при уменьшенных вдвое (до 0,125 мм) размерах элементов первых двух слоев. Общее число узлов возросло при этом до 86719, время решения – до 25 мин. Результаты, однако, оказались весьма близкими к результатам первого численного эксперимента: потери по слоям: 2,1203 Вт/мм, 0,7623 Вт/мм, 0,1312 Вт/мм, общие потери – 3,0138 Вт/мм. Выполненная проверка показала, что дробность сетки конечных элементов в исходной модели достаточна.

Доступные в настоящее время широкому пользователю конечно-элементные программы, например, FEMM [2-20, 2-21], позволяют рассчитывать потери в массивных сердечниках, возникающие в переменном электромагнитом поле. Потери при этом находятся в результате решения двухмерной полевой задачи при достаточно подробном воспроизведении конфигурации области и источников поля, при заданных свойствах материала массива и частоте питания. Основное допущение при решении нелинейных задач состоит в том, что для массива используется приближенная эквивалентная зависимость B(H).

Решение подобных задач, может занимать довольно большое время, особенно при недостатке опыта в таких расчетах. В то же время, полученное решение не всегда удобно для анализа конструкции, например, оно не позволяет оценить долю участия в общих потерях той или иной пространственной гармоники МДС обмотки.

В связи со сказанным представляется весьма желательным создание простых конечно-элементных моделей, позволяющих с достаточной для практических целей точностью и достаточно быстро получить оценку потерь в массиве, в том числе, потерь от отдельных гармоник МДС.

Ниже описывается несколько таких моделей и оценивается точность каждой из них. В качестве иллюстрации моделируется простая электрическая машина с сосредоточенной обмоткой, однако выводы могут быть распространены и на машины со сложными обмотками.

Модель №1. (Рис. 2.41). Первый сердечник (статор) представлен одним периодом трехфазной обмотки (2τ₁ = 360 мм). Относительная магнитная проницаемость сердечника взята достаточно большой (μ_r = 10⁴), чтобы практически удовлетворялось обычно принимаемое при аналитических выводах допущение μ = ¥. Пазы – открытые (Z = 6, q = 1), глубина пазов h_п равна 40 мм, токовой части пазов h_п_i - 30 мм, ширина пазов b_п – 10 мм. Статор шихтованный, электропроводность σ₁ его равна нулю. Зазор между статором и гладким массивным вторым сердечником (ротором) δ равен 2 мм. В качестве материала ротора выбрано мягкое железо (материал Pure iron из библиотеки материалов программы FEMM, электропроводность σ₂ = 10 МСм/м). На токовых участках пазов модели заданы плотности тока, соответствующие начальным и конечным катушечным сторонам фаз: A, Z, B, …, амплитуда плотности тока равна 5 А/мм² и, таким образом, максимальный ток паза равен 1500 А. На верхней и нижней границах модели заданы условия Дирихле (А = 0, А – векторный магнитный потенциал), на левой и правой границах – периодические граничные условия.

Возможна модификация модели – материал сердечника статора не воспроизводится, а на зубчатой его поверхности, след которой в этом случае является внешней границей области, задается условие Неймана. Результаты, полученные при такой замене, практически совпадают.

Модель №2. Отличается от модели №1 только тем, что плотности тока заданы не внутри пазов, а на узких, шириной Δi = 0,1 мм, участках, вынесенных в раскрытия пазов. Для сохранения значений пазовых токов плотности тока на этих участках увеличены в h_пi/Δi = 30/0,1 = 300 раз.

Модель №3.Отличается от модели №2 тем, что пазы не воспроизводятся, оба сердечника - гладкие.

Модель №4. Отличается от модели №3 тем, что пазовые токи заданы не в виде узких полос с постоянной плотностью тока в них, а в виде «точечных» токов, т.е. в виде линейных токов в проводах с бесконечно малым поперечным сечением. Располагаются точечные токи в центрах сечений полос модели №3.

Модель №5. Отличается от модели №3 тем, что узкие полосы, на которых заданы пазовые токи, имеют длину, равную не ширине паза, а ширине пазового деления. Плотность тока при этом по сравнению с моделью №3 уменьшена в t_z/b_п = 60/10 = 6 раз.

Модель №6. В этом случае, в отличие от модели №5, число участков с постоянной плотностью тока увеличено в 4 раза – ширине каждого пазового деления соответствуют 4 участка, причем фазовый сдвиг плотностей тока на соседних участках составляет 2π/(Z·4) = 2π/24. Таким образом, в этой модели обмотка воспроизводится сплошным токовым слоем толщиной Δi = 0,1 мм, расположенным на поверхности первого сердечника и состоящим из 24 участков с заданными на них плотностями тока, сдвинутыми по временной фазе на 1/24 периода (на рис. 2.42 стрелочками показаны векторы плотности тока на малых участках). Плотности тока в этом случае рассчитываются таким образом, чтобы мгновенное значение тока на пазовом делении было равно пазовому току в модели №1.

Модель №7. Отличается от моделей №1 и №2 тем, что токи обмотки заданы в виде токового слоя, состоящего из довольно большого (N_уч = 360) числа точечных токов. Значения каждого элементарного тока вычисляются по аналитическим выражениям для гармонических составляющих МДС обмотки и по выражениям, связывающим распределение скалярного магнитного потенциала по поверхности сердечника с линейной плотностью поверхностного тока [2-22].

Модель №8. Отличается от модели №7 тем, что пазы статора не воспроизводятся и оба сердечника – гладкие.

В моделях №7 и №8 амплитуды гармоник МДС рассчитывались как с учетом введенного Т.Г. Сорокером коэффициента влияния пазов C_ν [2-22],так и без такого учета.

Назад Продолжение