Расчет полей-2.3

Применение полевых методов в электромагнитных расчетах электрических машин

2.3. Конечно-элементное моделирование асинхронных двигателей с массивным ротором

( 1 2 )

С помощью простых конечно-элементных моделей можно весьма эффективно исследовать такие непростые с точки зрения электромагнитного анализа машины, как асинхронные двигатели с массивным ротором. Сложность электромагнитного расчета этих машин связана, как известно, с тем, что переменное поле в роторе должно быть определено с учетом нелинейных свойств стали и с учетом реакции токов, индуктированных в роторе, распределение которых в массиве ротора, в свою очередь, носит весьма сложный характер.

Большинство известных конечно-элементных программ позволяют пользователю находить приближенные решения полевых задач, связанных с возникновением в массивных средах, в том числе нелинейных, вихревых токов. В частности, программа FEMM позволяет решать задачи, в которых токи источников поля изменяются по гармоническому закону (т. наз. time-harmonic problems). При этом предполагается, что и все величины электромагнитного поля (напряженность и индукция магнитного поля, плотность тока) в каждой точке пространства изменяются во времени также по гармоническому закону. Это допущение предполагает замену действительной кривой намагничивания ферромагнитного материала среды некоторой эквивалентной кривой, для которой значению напряженности поля ставится в соответствие амплитуда основной гармоники временной зависимости индукции, рассчитанной по заданной действительной кривой намагничивания в предположении, что напряженность изменяется по синусоидальному закону. Соответственно этому вводится эквивалентная магнитная проницаемость среды μ_eff. В добавление к эквивалентной кривой намагничивания вводится понятие фазового угла гистерезиса (hysteresis lag), пропорционального магнитной проницаемости [2-18 и 2-19]. Переход к синусоидально изменяющимся во времени величинам поля позволяет сформулировать задачу в терминах комплексного векторного магнитного потенциала, что существенно облегчает ее решение.

При расчете переменного поля в массивном нелинейном ферромагнетике решается уравнение более сложное, чем при решении нелинейной магнитостатической задачи – в правой части уравнения появляется производная от векторного магнитного потенциала по времени. Следствием этого является то, что расчет таких полей занимает значительно больше времени, чем магнитостатических. Для выполнения приближенных быстрых расчетов, необходимость в которых обычно возникает на ранней стадии проектирования, удобно иметь линейную модель массивного ротора. Создать такую модель можно, представив цилиндрический ротор в виде многослойной структуры с постоянной магнитной проницаемостью в каждом слое. Значения магнитных проницаемостей слоев можно подобрать последовательными приближениями, имея в качестве базового решение задачи при воспроизведении нелинейных свойств материала ротора. При дальнейших расчетах полученную линейную модель можно использовать для приближенной оценки изменения размеров, схемы обмотки, плотности тока в обмотке и т.д.

Ниже приводится пример формирования линейной модели асинхронного двигателя с массивным ферромагнитным ротором на основе расчета поля при воспроизведении реальных нелинейных свойств ротора.

Смоделируем асинхронный двигатель с массивным ротором.

Некоторые данные двигателя и модели: диаметр расточки - 60 мм, зазор - 1 мм, обмотка однослойная, 2р =2, при моделировании зададим нелинейные характеристики стали статора (электротехническая сталь, сердечник шихтован) и ротора (мягкое железо, массив).

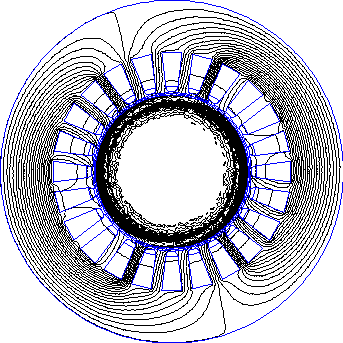
Рис. 2.26. Картина поля в поперечном сечении при заторможенном роторе и частоте питания 50 Гц

Амплитуда плотности тока в обмотке статора – 5 А/мм² (при моделировании переменных полей на участках пазов модели задаются комплексные значения плотности тока). Число узлов модели – 21813, время счета – ок. 25 мин.

Некоторые результаты моделирования: индукция в ярме статора – ок.0,5 Т, максимальная индукция в зубцах – ок.0,86 Т, максимальная индукция в роторе – ок. 2,6 Т (относительная магнитная проницаемость у поверхности ротора – ок. 60).

Рис. 2.27. Фрагмент картины поля. Индукция внутри массива ротора (но вблизи его поверхности) имеет в основном тангенциальную составляющую, изменяется по закону, близкому к синусу, с амплитудой ок. 2,6 Т.

Глубина поверхностного слоя, в котором индукция изменяется от 2,6 Т до 0,5 Т, составляет примерно 5 мм. Относительная проницаемость при этом возрастает от 60 до 13000 (материал ротора взят из библиотеки материалов программы FEMM – Pure Iron).

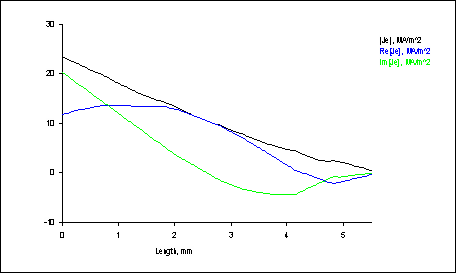
Рис. 2.28. Распределение плотности тока в поверхностном слое ротора (в зоне максимальной индукции). Максимальное значение действительной составляющей – ок. 14 А/мм², на глубине примерно 1,5 мм.

Основная гармоника распределения нормальной составляющей индукции в зазоре, найденная в результате гармонического анализа, равна 0,244 Т, Постоянная составляющая электромагнитногой момента, определенная интегрированием по контуру, проведенному посередине воздушного зазора, равна 0, 0237 Нм/мм.

Смоделируем теперь тот же двигатель, задав линейные характеристики стали ротора. Относительную проницаемость стали зададим равной 1000 и для статора, и для ротора. Сердечник статора будем считать шихтованным, ротор - массивным, с такой же удельной электропроводностью, что и в предыдущем случае – 10 МСм×м^-1.

Рис. 2.29. Картина поля в поперечном сечении двигателя с массивным ротором при линейных характеристиках стали статора и ротора (относительная магнитная проницаемость равна 1000)Т.

Назад Продолжение