Число фаз		3	5
Число пазов на статоре		15	15
Общее число узлов модели		41419	41604
Число слоев конечных элементов в зазоре		4	4
Материал постоянных магнитов , = 0,95, Нс = 1000000 А/м		-	-
Марка стали сердечника		core	core
Максимальная плотность тока на пазовых участках модели, А/мм2	Jмод	5	5
Максимальная индукция в зубцах, Т	Bz.max	1,72	1,74
Максимальная индукция в ярме статора, Т	Ba.max	1,33	1,8
Угловой интервал при моделировании поворота ротора, град	Δαрот	2	2
Число рассмотренных положений ротора	Nα рот	10	10

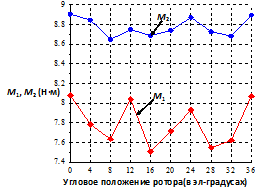
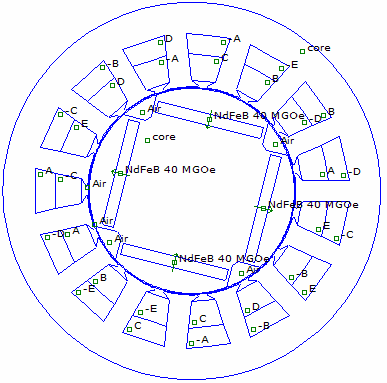
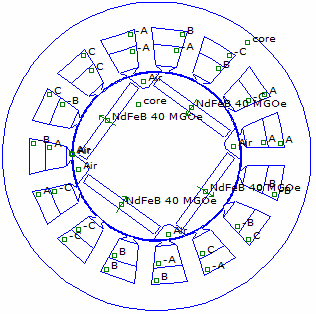
Рис. 2.23. Сравнение зависимостей момента для двигателей, модели которых показаны на рис. СТ15.  М₁ – для 3-фазного двигателя (15 пазов , q=5/4), М₂ – для пятифазного двигателя (15 пазов , q=3/4)

 

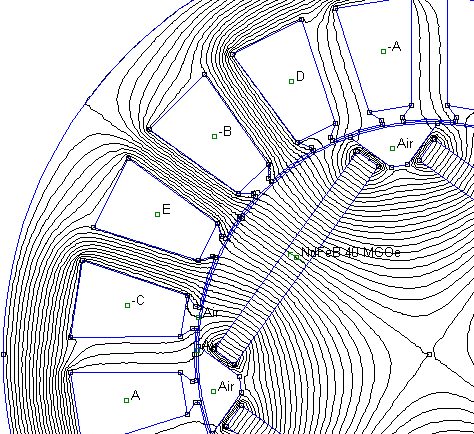
Рис. 2.24. Магнитное поле при отсутствии тока в обмотке статора пятифазного двигателя с постоянными магнитами на роторе (20 пазов , q=1) (фрагмент)

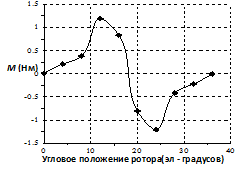
Рис. 2.25. Зависимость момента при отсутствии тока в обмотке статора (зубцовые пульсации момента) пятифазного двигателя с магнитами на роторе и двухслойной обмоткой на статоре (20 пазов, q=1)

Таблица 2.11

Сравнение пульсаций момента при различных моделей

 (по данным [2-14])

Для исследования зубцовых пульсаций момента применялись не только экспериментальные методы (имеются в виду как физические, так и численные эксперименты), но и аналитические методы [2-15 ÷ 2-17].

В [2-15] описан полуаналитический метод оценки зубцовых пульсаций момента при проектировании, на стадии выбора числа пазов сердечника. Предлагается при известных (выбранных) размерах паза, зазора и диаметра расточки выполнить конечно-элементную модель, на которой представлен зубчатый сердечник (например, статор) с одним пазом и второй сердечник (ротор) с постоянными магнитами. Рассчитав поле и найдя момент при достаточно большом числе взаимных положений сердечников, предлагается выполнить гармонический анализ полученной зависимости и затем на основе разработанного авторами [2-15] алгоритма рассчитать зависимость момента от угла поворота ротора для любого выбранного числа пазов. 

В [2-16 и 2-17] для расчета поля в зазоре машины с постоянными магнитами на одном из сердечников используется метод конформных преобразований, причем в [2-17] применяется четырехкратное преобразование. Рассчитанные по полученным аналитическим выражениям зубцовые пульсации момента по форме хорошо совпадают с найденными в конечно-элементном численном эксперименте, но по амплитуде заметно отличаются от них (в приведенных примерах расхождение составляет 30-40 %%). Тем не менее, полученные в [2-17] аналитические выражения позволили авторам оценить влияние различных изменений конфигурации зубцовой зоны на пульсации момента.